Traditional Machine Learning
传统机器学习方法
传统机器学习方法
User-CF适用于发现热点以及跟踪热点趋势。(user的爱好经常变动,相似度也会随之变动,而且容易受社交关系影响)
Item-CF适用于兴趣变化较为稳定的应用。(item相似度比较稳定)
缺点:泛化能力弱:无法将两个物品相似这一信息推广到其他物品的相似性计算上。导致热门的物品有很强的头部效应,容易根大量物品产生相似性,尾部物品则因为特征向量稀疏很少与其他物品产生相似性。
缺点: 用户数往往大于物品书,用户数的增长会导致用户相似度矩阵的存储空间以\(n^2\)的速度快速增长。
\[ similarity=cos(\theta) = \frac{A\cdot B}{||A||\space ||B||} \]
\(R_{i,p}\): 用户i对物品p的评分。
\(\bar{R_i}\): 用户对所有物品的平均评分。
\[ sim(i,j)=\frac{\sum_{p\in P}(R_{i,p}-\bar R_p)(R_{j,p}-\bar R_p)}{\sqrt{\sum_{p\in P}(R_{i,p}-\bar R_p)^2}\sqrt{\sum_{p\in P}(R_{j,p}-\bar R_p)^2}} \]
\(R_{i,p}\): 用户i对物品p的评分。
\(\bar{R_p}\): 物品p的平均分。
\[ R_{u,s}=\frac{\sum_{s\in S}(w_{u,s}\cdot R_{s,p})}{\sum_{s\in S}w_(u,s)} \]
\(w_{u,s}\): 是用户u和用户s的相似度
\(R_{s,p}\): 是用户s对物品p的评分。
计算相似度后(计算方法与user相同),用下面式子计算: \[ R_{u,p}=\sum_{u\in H}(w_{p,h},\cdot R_{u,h}) \] \(w_{p,h}\): 是物品p与物品h的相似程度。
\(R_{u,h}\): 是用户u对物品h的已有评分。
协同过滤的进化
优点:
缺点:没有考虑用户与物品的其他特征。
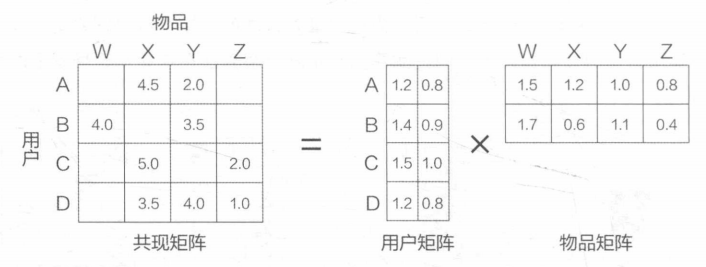
通过分解共现矩阵学习用户和物品的表示。
将(m,n)维的共现矩阵M分解为(m,k)维的用户矩阵和(k,n)维的物品矩阵,其中相应的行和列为特定用户与物品的表示,k是用户和物品表示的维度。
预测方法:用户表示与物品表示的内积。 \[ r_{ui}=q_i^Tp_u \]
特征值分解只能用于方阵,所以用特征值分解
矩阵分解—特征值分解与奇异值分解 - 知乎 (zhihu.com)
通过奇异值分解求得\(M=U\sum V^T\),其中\(U\in (m,m),\sum \in (m,n),V^T\in (n,n)\),中间的为对角阵
取\(\sum\)中较大的k个元素为隐含特征,删除其他维度(U与V中的也删掉)
得到\(M=U_{m\times k}\sum_{k\times k} V^T_{k\times n}\)
缺点:
奇异值分解要求原始的共现矩阵是稠密的,如果要使用奇异值分解,就必须对确实的元素值进行填充。
复杂度高O(mn^2)
主要方法
Loss: \[ L=min_{q^*,p^*}\sum (r_{ui}-q_i^Tp_u)^2+\lambda(||q_i||^2+||p_u||^2) \] 由于不同用户打分标准不同,加入偏差 \[ r_{ui}=\mu +b_i+b_u+q^T_ip_u \] \(\mu\): 全局偏差常数,超参数,提前设置好
\(b_i\): 物品偏差系数,可以使用物品i收到的所有评分的均值
\(b_u\): 用户偏差系数,可以使用用户u给出的所有评分的均值 \[ L=min_{q^*,p^*}\sum (r_{ui}-q_i^Tp_u-\mu-b_u-b_i)^2+\lambda(||q_i||^2+||p_u||^2+b_u^2+b_i^2) \]
独立于协同过滤的推荐模型方向
将用户年龄、性别、物品属性等特征转为数值型向量输入回归或逻辑回归模型
优点:融合了特征
缺点:逻辑回归模型简单,表达能力不强
逻辑回归只对单一特征做简单加权,不具备特征交叉生成高维组合特征的能力 \[ POLY2(W,X)=\sum_{j_1=1}^{n-1} \sum_{j_2=j_1+1}^nw_h(j_1,j_2)x_{j_1}x_{j_2} \] POLY2就是直接暴力组合特征,\(x\)是未经embedding处理的特征(one-hot 或 数值特征)
缺点:
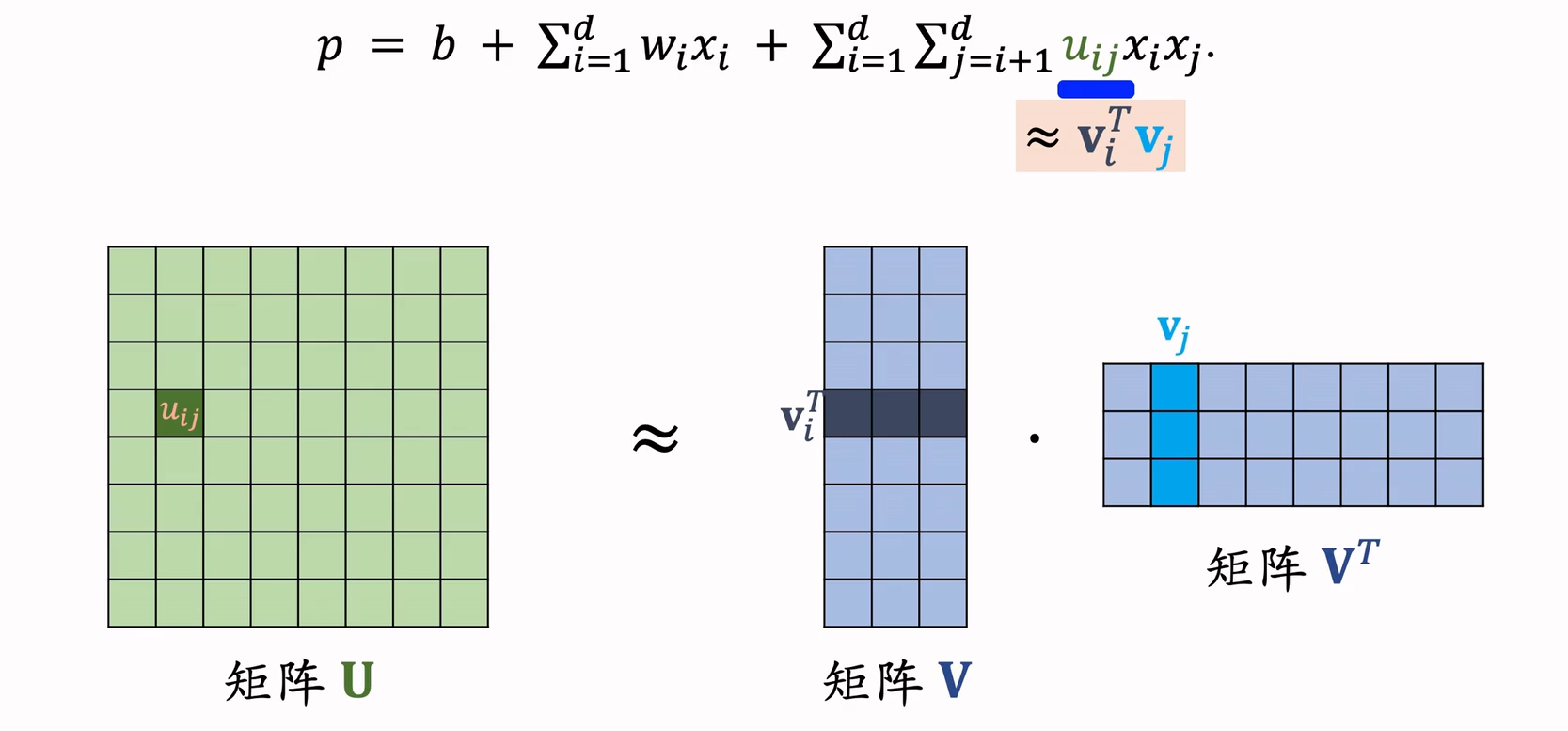
FM为给个特征学习了一个隐权重向量,在特征交叉时,使用两个特征隐向量的内积作为交叉特征的权重。下面是二阶的数学部分: \[ FM(w,x)=\sum_{j_i=1}^{n-1} \sum_{j_2=j_1+1}^n (w_{j_1}\cdot w_{j_2})x_{j_1}x_{j_2} \] 我们也可以看作是将POLY2方法中\(R^{n\times n}\)的矩阵分解为两个矩阵\(R^{n\times k}\)和\(R^{k\times n}\),其中第一个矩阵第i行与第二个矩阵第j列相乘即使特征i、j的特征交叉参数。
优点:
缺点:
FFM每个特征对应的不是唯一一个隐向量,而是一组隐向量。特征作用于不同的特征域有不同的隐向量:特征1与特征2交叉,则是特征1作用于特征域2:\(w_{j_1,f_2}\)乘特征2作用于特征域1:\(w_{j_2,f_1}\) \[ FFM(w,x)=\sum_{j_i=1}^{n-1} \sum_{j_2=j_1+1}^n (w_{j_1,f_2}\cdot w_{j_2,f_1})x_{j_1}x_{j_2} \] 与FM区别:
下图中,P,下面是特征值

| ESPN特征与NIKE特征交叉 | ESPN特征与MALE特征交叉 | |
|---|---|---|
| FM | \(w_{ESPN}\cdot w_{NIKE}\) | \(w_{ESPN}\cdot w_{MALE}\) |
| FFM | \(w_{ESPN,A}\cdot w_{NIKE,P}\) | \(w_{ESPN,G}\cdot w_{MALE,P}\) |
计算复杂度:需要学习n个特征在f个特征域上的k维隐向量,参数数量:\(n\cdot k\cdot f\),二次项不能像FM一样简化,复杂度是\(kn^2\)。
注意,n>f,一个特征域有可能有多个特征,例如性别特征域有两种特征:男和女。我们只需要学习NIKE特征在性别特征域的1个隐向量,不需要具体学习NIKE对男性的隐向量或NIKE对女性的。这样参数量还是比POLY2少很多。
POLY2,再提高交叉维度会产生组合爆炸。
GBDT+LR:就是利用GBDT自动进行特征筛选和组合,生成新的离散特征向量,再把特征向量当做LR模型输入。
以前特征组合要么人工筛选,要么通过改造目标函数筛选,GBDT+LR实现了end2end用模型筛选。
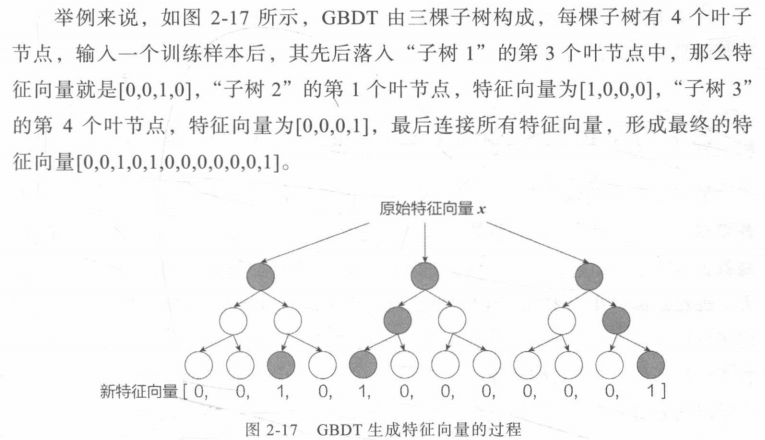
决策树的每一层都在划分重要特征(划分后label纯度提高),如果决策树深度为2层则意味着抉择树挑选了两个重要特征进行特征交叉。
训练sample在输入GBDT的某一子树后会根据每个节点的规则落入叶子节点,把所有叶子节点组成的向量为该棵树的特征。
e.g.
参考:经典推荐算法学习(四)| 阿里LS-PLM(MLR)模型原理解析 - 知乎 (zhihu.com)
在逻辑回归的基础上加入分片的思想,其灵感来自对广告推荐领域样本特点的观察。
举例来说,如果CTR模型要预估的是女性受众点击女装广告的CTR,那么显然,我们不希望把男性用户点击数码类产品的样本数据也考虑进来,因为这样的样本不仅与女性购买女装的广告场景毫无相关性,甚至会在模型训练过程中扰乱相关特征的权重。
其实就是一个类似attention结构去捕捉用户的兴趣。
公式如下: \[ p(y=1|x) = g(\sum_{j=1}^m\sigma(u_j^Tx)\eta(w_j^Tx)) \]
\[ p(y=1|x)=\sum_{i=1}^m\frac{exp(u_i^Tx)}{\sum_{j=1}^mexp(u_i^Tx)}\cdot \frac{1}{1+exp(-w_i^Tx)} \]
如上述公式所示,LS-PLM在表达上非常朴实,拆开来看就是常见的softmax和LR 。\(u^T,w^T\)是可训练参数
\(sigma(u_j^Tx)\) :SoftMax部分,负责将特征切分到m个不同的空间。
\(\eta(w_j^Tx)\) :LR部分则负责对m个空间的特征分片的进行预测
\(g(\cdot )\) :sigma函数,作用则是使得模型符合概率函数定义。
通过控制分片数m,使得LS-PLM便具备拟合任意强度高维空间的非线性分类面能力。
如图1,假设训练数据是一个菱形分类面,基于LR的模型能做到的效果如图1.B),LS-PLM则可以做到用4个分片完美的拟合训练集合,如图1.C)。
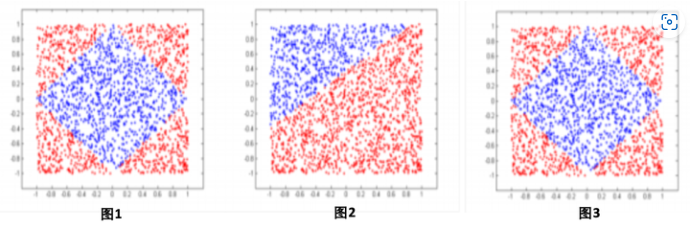
可以简单理解为通过前面的softmax部分把sample分到不同的LR function去进行计算,就可以拟合出上图结果
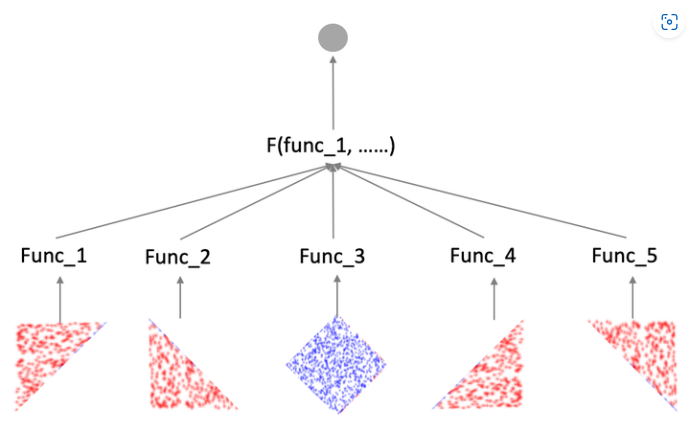
但m增加则容易过拟合,一般阿里选m=12.
引入L1正则化进行得到稀疏解,引入L2,1正则化提高泛化能力避免过拟合
利用协同过滤中的共现矩阵,完成物品向量或者用户向量的自编码。
假设有m个用户n个物品,我们能得到一个(m,n)的评分矩阵。
对于物品i,所有m个用户对它的评分可以行程一个m维向量r,构建一个三层网络:
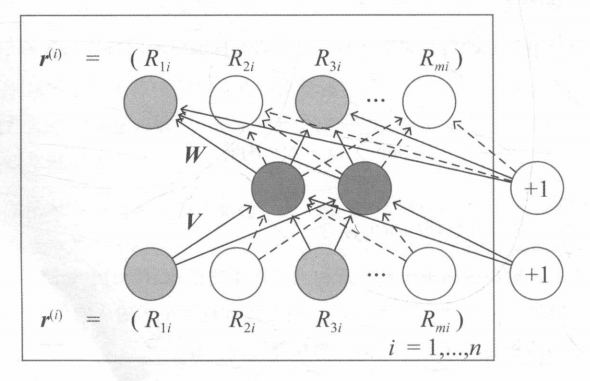 \[
h(r,\theta) = f(W\cdot g(Vr+\mu)+b)
\] g,f为激活函数
\[
h(r,\theta) = f(W\cdot g(Vr+\mu)+b)
\] g,f为激活函数
Loss function: \[ Loss=min_\theta^n||r^{(i)}-h(r^{(i)},\theta)||^2+\frac{\lambda}{2}(||W||_F^2+||V||_F^2) \]
当输入物品i评分向量\(r^{(i)}\)时,模型输出\(h(r^{(i)},\theta)\)就是所有用户对物品i的评分,那么其中的第u维就是用户u对物品i的预测. \[ R_{ui} = (h(r,\theta))_u \] 其实就是一个泛化过程,重建函数\(h(r,\theta)\)中存储了所有数据向量的精华,经过自编码器生成的输出向量不会完全等同于输入向量,所以会具备了一定的缺失维度的预测能力。
把用户评分向量作为输入向量,但是用户向量稀疏性可能会影响模型效果。
传统矩阵分解欠拟合,因为score层太简单
将矩阵分解(CF的扩展)中的scoring层用多层神经网络取代
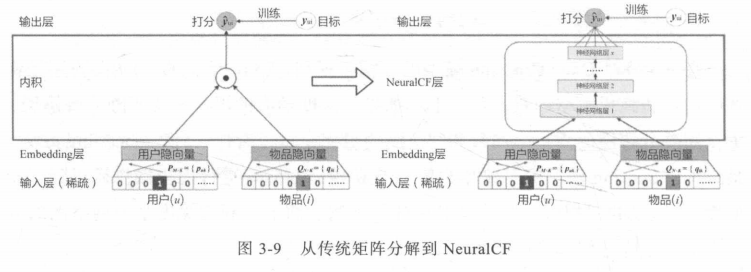
NeuralCF还提出了将传统矩阵分解方法和深度学习方法融合的模型:
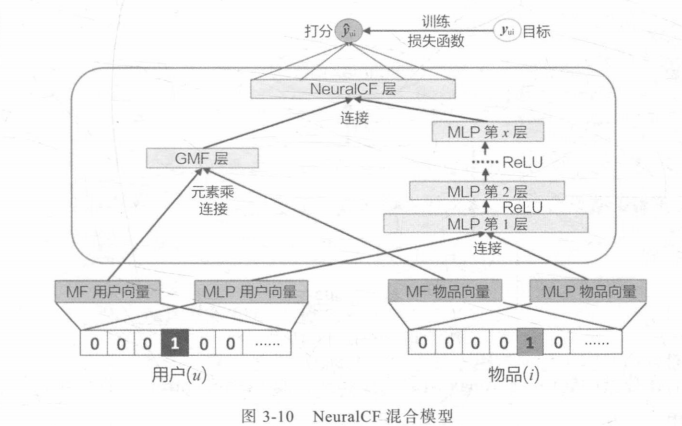
左边MF为传统矩阵分解学习的向量,通过元素积让向量在各个维度上成分交叉(取代原来的直接内积);
右边则是深度学习矩阵分解,最后将两个处理后向量连接再进行评分。
输入特征:
可以被处理为one-hot或者multi-hop的类别特征
数组特征
需要进一步处理的特征
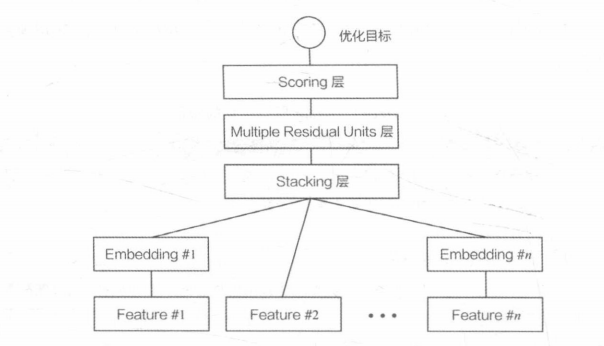
模型结构:
意义:
利用乘积层(Product Layer)取代了DeepCrossing中的Stacking层。
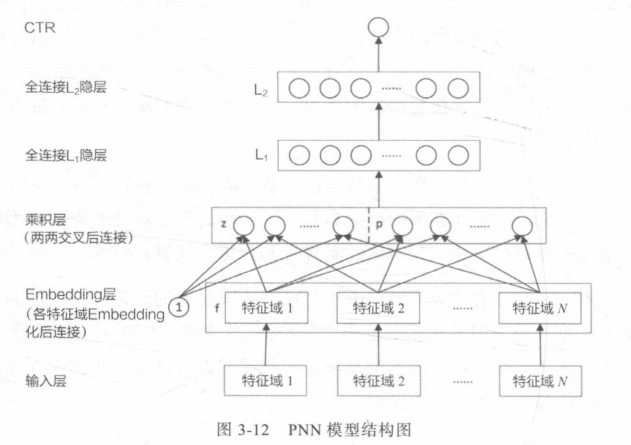
不同特征的Embedding不再是简单的拼接,而是在Product层进行两两交互,更有针对性的获取特征之间的交互信息。
乘积特征交叉部分又分为内积操作IPNN和外积OPNN操作,其中OPNN在进行外积后得到的是一个矩阵,PNN把所有两两特征Embedding向量外积互操作的结果叠加进行降维。IPNN则是内积得到一个值后concatenate后变成一个向量。
优点:
加强不同特征之间交叉交互。
缺点:
OPNN中粗暴的简化操作可能会丢失信息。
无差别价差特征一定程度上忽略原始特征向量中包含的有价值的信息。
wide-让模型更有记忆能力-模型结构简单,原始数据王位可以直接影响推荐结果。
记忆能力可以理解为模型直接学习并利用历史数据中物品或者特征的“共现频率”能力(哪些关键特征会直接导致什么必然结果,e.g.如果点击过A则大概率会点击B)
deep-让模型更有泛化能力
泛化能力可以理解为模型传递特征的相关性以及挖掘稀疏甚至从未出现过的稀有特征与最终标签相关性的能力。
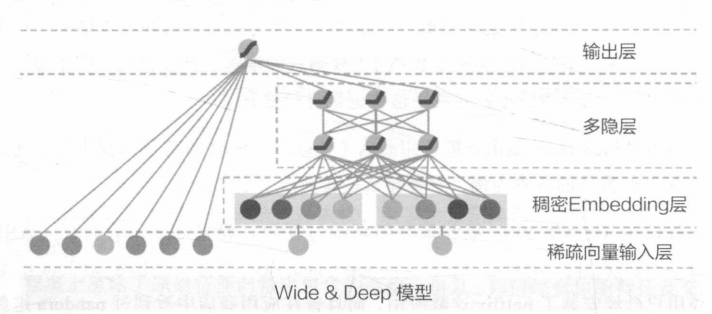
什么特征输入到Deep什么输入到Wide需要深刻理解应用场景后人工设计,例子:
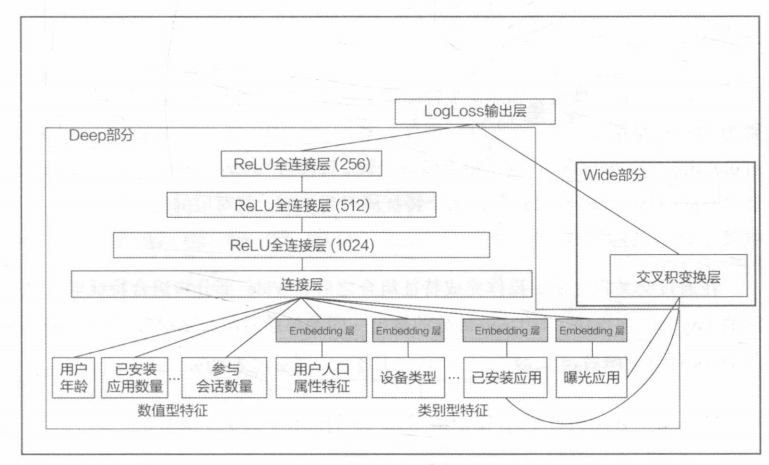
所有特征都被输入到Deep去挖掘深层次关系,只有已安装应用和曝光应用这种直接粗暴对结论有重要直接影响的特征。
在Wide层,Geogle用的交叉积变换处理:
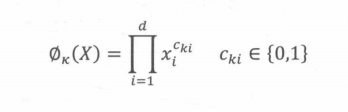
\(c^{ki}\)是一个布尔变量,当第i个特征属于第k 个组合特征时,c的值为1,否则为0;
x是第i个特征的值。
例如,对于“AND(user_installed app=netflix.impression app=pandora)”这个组合特征来说只有当“user installed app=netflix和“impression_app=pandora”这两个特征同时为1时,其对应的交叉积变换层的结果才为1,否则为0。
用Cross网络取代Wide&Deep中原来Wide部分,Deep部分没变。
Cross网络能增加特征之间的交互力度
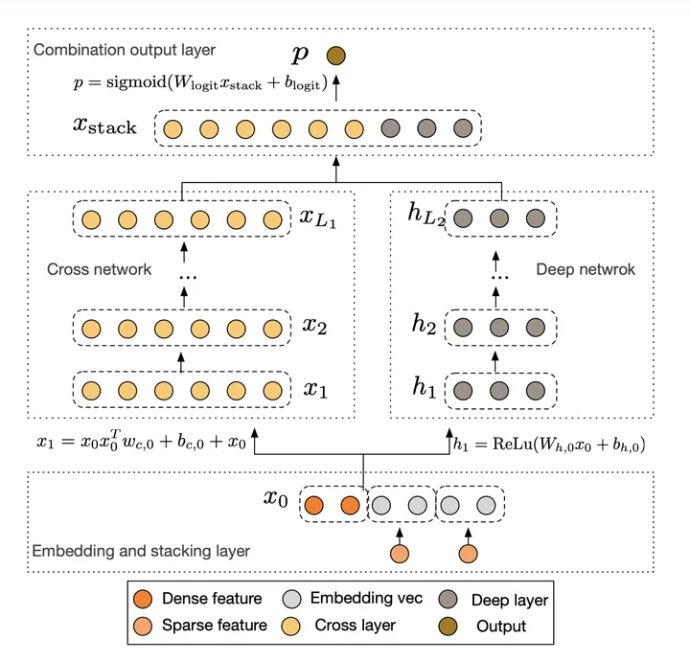
Cross网络使用多层交叉层,假设第l层输出为\(x_l\),那么第l+1层输出为: \[ x_{l+1}=x_0x_l^TW_l+b_l+x_l \] 这里的\(x_0\)是将所有输入特征处理好之后concatenate起来的一个向量,不同的维度代表不同的特征。
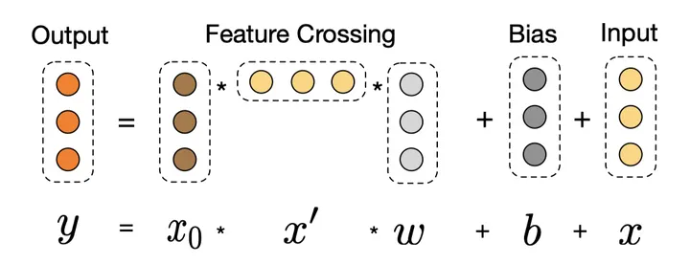
cross layer的每一层其实是将两个向量A、B矩阵相乘为一个矩阵M,\(M_{ij}\)代表A向量的第i维度与B向量第j维度相乘,这样就将两个向量的每个维度两两相乘,而向量\(x_0\)中的不同维度代表不同特征,也就是让不同特征充分交互。
cross network为1层的时候,我们可以得到的最高是2维的特征交叉;cross network为2层的时候,我们得到的是最高3维的特征交叉;cross network为3层的时候,我们得到的是最高4维的特征交叉;以此类推。。。
因此cross network以一种参数共享的方式,通过对叠加层数的控制,可以高效地学习出低维的特征交叉组合,避免了人工特征工程。
交叉后过一个MLP层,最后再加上交叉前的l层输入,其实就是为了学习残差。
propose DHGCN,2HRDR
relation-enhance KG
Hypergraph knowledge graph
Relation work of DHT
Hypergraph
Some simple knowledge of PyG