Traditional Machine Learning

Posted on Edited on In ,

传统机器学习方法

Tree

Single Tree

Decision Tree

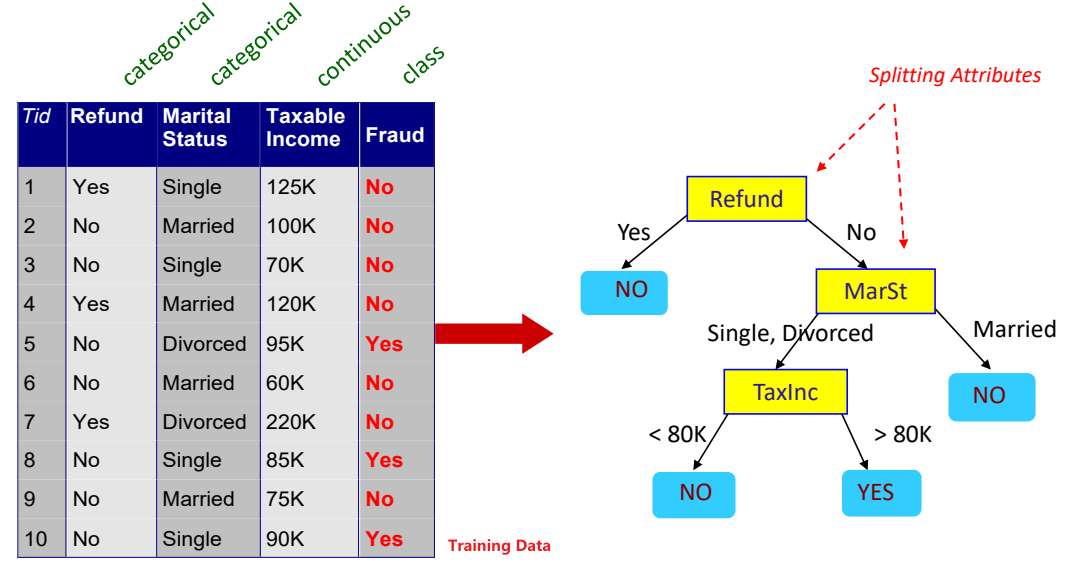
image-20230712165541790

决策树重点：挑选重要的特征，越重要的特征放的越接近根节点。

ID3

ID3算法使用Information Gain信息增益作为挑选特征指标。

Entropy-熵

在数学与物理上，熵指混乱程度，或者说值得是变量X的自由度和不确定性。

在计算机理论中，熵度量给定数据中的杂质。 \[ Entropy(p)=\sum_{i=1}^C-p_i*log_2(p_i) \] c : 可能出现的种类数量

\(p_i\)：第i类的概率

熵越小，数据越纯

example:

image-20230712174626803
Information Gain

Information Gain计算拆分前后熵的变化，即用拆分特征前的熵减去拆分特征后的平均熵。 \[ Information Gain = Entropy(entire\_dataset)-\frac{1}{n}\sum_{i=1}^n Entropy(child\_dataset_i) \] 上面式子表示将整个数据集依照某个特征值拆分为了n个子数据集。

example:

也可以

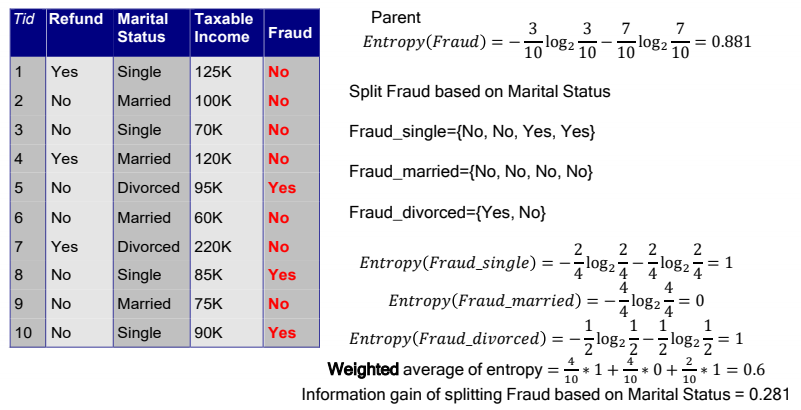
有的教程会写作：熵减去条件熵

简单认识一下条件熵就好，起码知道词是个啥子意思嘛

熵是对事件结果不确定性的度量，但在知道有些条件时，不确定性会变小。这里的条件就是数据集中的特征。

条件熵就是已知某个特征X的情况下，事件Y的不确定性 \[ Entropy(Y|X)=\sum_{i=1}^np_i Entropy(Y|X=x_i) \] 就是特征X每个可能性的结果的熵乘以发生概率的求和。 \[ Information Gain = Entropy(Y)- Entropy(Y|X) \]

ID3缺点
  1. 没有剪枝策略，容易过拟合。
  2. 只能用于处理离散分布的特征。
  3. 没有考虑缺失值。
  4. InformationGain对可取数值数目较多的特征有所偏好，类似‘ID’的特征其信息增益接近于1。

C4.5

使用Information Gain Ratio信息增益率作为挑选指标，减少因特征值类别多导致信息增益大的问题。同时引入了剪枝策略。

Information Gain Ratio

\[ IGR = \frac{IG(feature,dataset)}{Entropy(feature)} \]

Entropy(feature): 特征的固有值，即是特征的纯度，（之前求得都是label的熵）公式如下： \[ Entropy_A(dataset) = -\sum_{i=1}^np_i*log_2(p_i) \] c : A中可能出现的种类数量

\(p_i\)：A为第i类的概率

这能解决ID3的第四个缺点，特征可能类别越多（越细致），纯度低，熵越高，分母越大

剪枝策略

剪枝缓解决策树过拟合

预剪枝

生成决策树过程中剪枝

  1. 提前设定决策树的高度，当达到这个高度时，就停止构建决策树；
  2. 当达到某节点的实例具有相同的label，也可以停止树的生长；
  3. 提前设定某个阈值，当达到某个节点的样例个数小于该阈值的时候便可以停止树的生长，但这种方法的缺点是对数据量的要求较大，无法处理数据量较小的训练样例；
  4. 同样是设定某个阈值，每次扩展决策树后都计算其对系统性能的增益，若小于该阈值，则让它停止生长。

预剪枝的显著缺点是视野效果。因为剪枝是伴随着构建决策树同时进行的，构建者无法预知下一步可能会发生的事，会出现某种情况，在相同标准下，当前决策树不满足要求最开始的构建要求、构建者进行了剪枝，但实际上若进行进一步构建后、决策树又满足了要求。这种情况下，预剪枝会过早停止决策树的生长。

C4.5算法常选择后剪枝的方法消除决策树的过度拟合

后剪枝

在已经生成的决策树上剪枝

用递归的方式从低往上针对每一个非叶子节点，评估用一个叶子节点去代替这课子树是否有益。如果剪枝后与剪枝前相比其错误率是保持或者下降，则这棵子树就可以被替换掉。C4.5 通过训练数据集上的错误分类数量来估算未知样本上的错误率。

后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝决策树。但同时其训练时间会大的多。

优点

  1. 解决特征值类别多导致信息增益大的问题

  2. 引入剪枝

  3. 增加对连续特征值的处理：将连续特征离散化，假设 n 个样本的连续特征 A 有 m 个取值，C4.5 将其排序并取相邻两样本值的平均数共 m-1 个划分点，分别计算以该划分点作为二元分类点时的信息增益，并选择信息增益最大的点作为该连续特征的二元离散分类点；

  4. 增加对缺失值处理：

    1. 在特征值缺失的情况下进行划分特征的选择？（即如何计算特征的信息增益率）

      C4.5 的做法是：对于具有缺失值特征，用没有缺失的样本子集占整个数据集的比重来折算；

    2. 选定该划分特征，对于缺失该特征值的样本如何处理？（即到底把这个样本划分到哪个结点里）

      C4.5 的做法是：将样本同时划分到所有子节点。不过要调整样本的权重值，其实也就是以不同概率划分到不同节点中。

缺点
  1. 依然不能处理回归问题
  2. 使用的熵模型拥有大量耗时的对数运算，连续值还有排序运算；
  3. 用的是多叉树，用二叉树效率更高；
  4. 在构造树的过程中，对数值属性值需要按照其大小进行排序，从中选择一个分割点，所以只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时，程序无法运行。

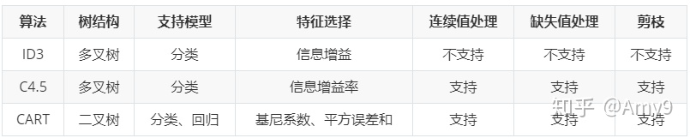
CART- classification and regression tree

CART是决策树的延伸，也可以看作特殊的决策树。他建立起来的是二叉树，而不是多叉树。

可以不仅可以解决分类问题，还可以觉得回归问题

image-20230717124658992

Classification

特征挑选指标：Gini index

基尼系数越小，纯度越高，特征越好。

Gini值

Gini值反应了从数据集D中随机抽取两个样本，其类别不一样的概率。 \[ Gini(D) = \sum_{i=1}^np(x_i)*(1-p(x_i))=1-\sum_{i=1}^np(x_i)^2 \] \(p(x_i)\): \(x_i\)出现的概率

n：类别数量

分类树的构造

递归生成二叉树，以Gini值最小化作为准则。

  1. 遍历所有特征\(A\),遍历特征\(A\)所有的可能取值\(a\)，根据特征A 是否取某一可能值a，把样本D分成两部分\(D_1\)和\(D_2\)。计算Gini值，将Gini值最小的\(A,a\)作为最优特征与最优切分点。 \[ D_1 = (x,y)\in D |A(x)=a,D_2 = D-D_1 \]

    \[ Gini(D|A=a) = \frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2) \]

  2. 循环1步骤

Regression

递归生成二叉树，使用平方误差最小化作为准则。

假设有n个样本\(D={(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)}\),其中x是d维向量，代表d个特征，y是连续值。

CART回归树生成算法：

  1. 遍历所有特征\(d_i\),遍历n个样本在\(d_i\)特征的取值x，取相邻两样本值x(排序后)的平均数s作为划分点，利用s作为划分两个区域的阈值： \[ R_1 = \{y_i|x_{i,d_i}<=s\},R_2 = \{y_i|x_{i,d_i}>s\} \] 每个区域内样本\(y_i\)的均值作为该区域的预测值\(c_1, c_2\)，计算样本真实值和预测值的平方误差之和,并找到能使平方误差最小的\(d_i\)和\(s\): \[ c_1 = \frac{1}{n}\sum_{x_i\in R_1}y_i,c_2 = \frac{1}{n}\sum_{x_i\in R_2}y_i, \]

    \[ \min_{d_i,s}\{\sum_{x_i\in R_1(d_i,s)}(y_i-c_1)^2+\sum_{x_i\in R_2(d_i,s)}(y_i-c_2)^2\} \]

  2. 重复1直到满足停止条件

  3. 最后划分为M区域\(R_1,R_2,\cdots,R_M\),生成决策树,预测值为： \[ f(x)=\sum_{i=1}^Mc_iI(x\in R_i) \] 这里的\(I(x\in R_i)\)值，满足条件返回值为1，否则为0

Several tree

Bagged Decision Tree

单棵的决策树高方差（不同训练集训练的预测结果差很多，不稳定），Bagged Decisoin Tree要解决这个问题。

使用Bootstrap生成多个训练集。它基于有放回地从原始训练数据集中抽取样本，构成一个新的训练集。通过对原始数据集的多次重采样，可以生成多个不同的训练集，每个训练集都是原始数据集的一部分。接着将每轮未抽取的数据合并形成袋外数据集（Out of Bag, OOB），用于模型中的测试集。

使用Bagging进行训练和预测。通过在 Bootstrap 生成的多个训练集上训练多个独立的基础模型，并将它们的预测结果进行平均或投票来进行最终预测。每个基础模型都是独立训练的，它们之间没有依赖关系。Bagging 可以减少模型的方差，提高模型的稳定性和泛化能力。

Random Forest

随机森林使用的方法与Bagged Decision Tree一样使用Bootstrap和Bagging方法，但做出了改进。

决策树使用的是贪心策略，每一步都是局部最优解，但每次的局部最优解不一定能得到全局最优解。而且Bagging后，我们可能会得到几个非常相似的局部最优解树。

所以随机森林加入随机策略，鲁棒性会更强。

构建随机森林

  1. 使用Bootstrap策略，有放回的抽取sample生成N个训练集，每个训练集可以训练出一个子模型。
  2. 训练单棵决策树
    1. 每个sample有M个特征，在决策树的每个节点需要分裂的时候，随机从M个特种中选取m个特征，满足条件m << M。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性。（这样让决策树不要过分关心一个重要特征，鲁棒性更强）
    2. 循环1步骤

GBDT

使用Boosting思想，以决策树为基函数的提升方法称为提升决策树。保证每棵树都是低方差，高偏差。

GBDT的原理、公式推导、Python实现、可视化和应用 - 知乎 (zhihu.com)

算法

!image-20230720171728041]