Data Structure and algorithms

Posted on Edited on In
  1. Complexity
  2. Linear structures
  3. Tree structures
  4. Other common data structures
  5. Search algorithms
  6. Sorting algorithms

Complexity

Array

fixed length, indexable, should shift after insertions and deletions

image-20230419185630699

Array Operation

Insertion O(n)

  1. insert an element in the specified index
  2. shift the subsequent item to the right

Deletion O(n)

  1. delete the specified element
  2. shift the subsequent item to the left

Searching in a sorted array

Best case-O(1)

Worst case-O(n)

Average case-O(n/2)->O(n)

Binary search O(logn)

Sorting array

image-20230419191311851

Stack

Last In First Out

Stack Operation

Push(S,x): insert x to the top of the stack S

Pop(S): extract the top of the stack S

Top(s): return the topmost element of stack S without removing it

isEmpty(s): return whether the stack S is empty

Implementation

Array

Push() O(1)

1
2
3
4
5
if s.top=s.len
	error 'full'
else
	s.top=s.top+1
	s[s.top]=x

Pop() O(1)

1
2
3
4
5
if isEmpty(s)
	error 'empty'
else
	s.top=s.top-1
	return s[s.top+1]

Top() O(1)

1
2
3
4
if isEmpty(s)
	error 'empty'
else
	return s[s.top]

isEmpty() O(1)

1
2
3
4
if s.len=0
	return true
else
	return false

Search O(n)

Use stack implements a simple calculator

  1. transfer to postfix notation

3-2-1>>32-1-

3-2*1>>321*-

  1. use stack to calculate

3-2-1>>32-1-

1
2
3
4
5
push(3)
push(2)
Meet(-);Pop;Pop;Push(3-2=1)
Push(1)
Meet(-);Pop;Pop;Push(1-1=0)
  1. exercise

10 + (44 − 1) * 3 + 9 / 2

((1 - 2) - 5) + (6 / 5)

(((22 / 7) + 4) * (6 - 2))

Queue

First In First Out

Operation

Enqueue(Q,x): put an element x at the end of queue Q

Dequeue(Q): extract the first element from queue Q

Implementation

Array 1

Enqueue in the tail -O(1)

Dequeue in the position0 -O(n)

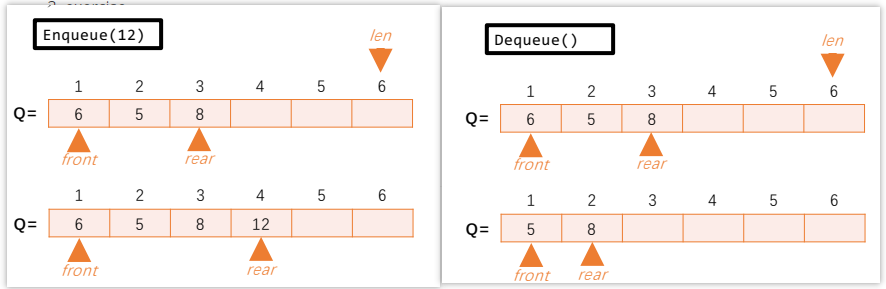
image-20230419194745117

Array 2

Enqueue in the position0 -O(n)

Dequeue in the tail -O(1)

image-20230419195104009

Array 3 -Circular queue

Enqueue: O(1)

Dequeue: O(1)

Peeking (get the front item without removing it) O(1)

isFull: O(1)

isEmpty: O(1)

search: O(n)

algorithm implement

Data members:

• Q: an array of items • Q.len: length of array • Q.front: position of the front item • Q.rear: rear item position + 1 (not an item)

Enqueue
1
2
3
4
5
6
7
8
if isFull(Q)
	error 'full'
else
	Q[Q.rear] = x
	if Q.rear==Q.len:
		Q.rear=1
	else
		Q.rear=Q.rear+1
Dequeue
1
2
3
4
5
6
7
8
if isEmpty(W)
	error 'Empty'
else
	x=Q[Q.front]
	if Q.front==Q.len
		Q.front=1
	else
		Q.front=Q.front+1
isFull and isEmpty
image-20230419201711632

Linked List

image-20230420110345241

Node: An object containing data and pointer(s) Pointer: Reference to another node Head: The first node in a linked list Tail: The last node in a linked list

image-20230420112447328

No limited to size

require more space per element

Initial

...

Operation

  1. print

  2. insert

  3. Delete

Hash table

Dictionary ADT

key:value

implement of ADT

array

Space usage: O(n)

Search usage: O(n)

Array index Key Value
0 3 Coffee
1 15 Bread
2 8 Tea

Large array

Space usage: O(U)-max key

Search usage: O(1)

Array index Key Value
... ... ...
3 3 Coffee
... ... ...
8 8 Tea
... ... ...
15 15 Bread

Hash table

Converts a key (of a large range) to a hash value (of a small range). e.g. k mod m

Space usage: O(n)

Search usage: O(1)

Collision solution

collision: different keys have the same hash value

Chaining
use a linked list
image-20230422183421651
load factor

\[ \lambda = \frac{n}{m} \]

n is the number of keys, m is the total number of buckets.

Measures how full the hash table is

it is suggested to keep \(\lambda\) < 1

cost

  1. time

    cost of search: O(1)+O(l), l is the length of the linked list

    worst case: O(1)+O(n)

    Average case: O(1)+O(\(\lambda\))

  2. space

    requires additional space to store the pointers in linked lists of entries.

    Worst case: n-1 additional space

    Average case: \(\lambda\)-1 additional space

Opening addressing: probing
Insert
image-20230422185347171
image-20230422185455352
Delete
image-20230422190114349
Load factor

must \(\lambda < 1\)

How to deal with the hash table when ! becomes large?

  1. Make a large hash table and move all elements into it.
  2. Simply add an additional hash table
probing type

  1. Linear probing

    \[ H(k,i) = (H_0(k) + i)\space mod \space m \] have clustering problem, multiple keys are hashed to consecutive slots.

    performance degrade significantly when \(\lambda\)> 0.5.

  2. Quadratic probing \[ H(k,i) = (H_0(k) + a\cdot i+b\cdot i^2)\space mod \space m \] reduces the clustering problem.

string key

image-20230422191105400

Tree

a tree is an abstract model of a hierarchical structure consists of a set of nodes and a set of edges.

Every node except the root has exactly one parent node.

Definition

  1. Length of a path： The number of edges in the path.

  2. The height of a node：

    The largest path length from that node to any leaf node (not including ancestors).

    Each leaf node has the height 0.

  3. The height of a tree: The maximum level of a node in a tree is the tree’s height.

  4. The depth of a node:

    The node's level (depth) of a node is the length of the path from that node to the root.

    The depth of the root is zero.

Binary Tree

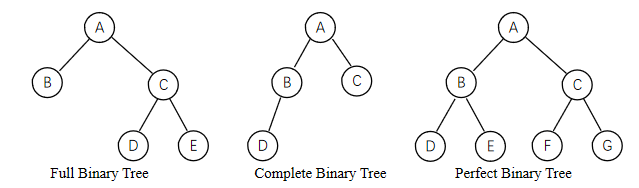
image-20230424201038461

Full Binary Tree

Every node has either 0 or 2 children.

Complete Binary Tree

Every level, except the last level, is completely filled, and all nodes in the last level are as far left as possible (left justified).

Perfect Binary Tree

Every node except the leaf nodes have two children and every level is completely filled.

image-20230424201302544

list representation: [Root, left-sub-tree, right-sub-tree]

Binary Search Tree

Insertion - O(h)

Search - O(h)

Deletion: O(h)

ℎ is O(log⁡n) if tree is balanced.

all is O(n) in worst case

左小右大

Search Operation

1
2
3
4
5
6
7
8
9
10
11
12
13
Algorithm SearcℎBST(t, target)
  Input: the BST t and the target

  p = t.root
  while p≠null do
      if target=p.value do
          return p
      else if target<p.value do
          p=p.left
      else
          p=p.rigℎt
  end
  return null

Insert

average case: O(n) = logn

worst case: O(n) = n

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Algorithm Insert(t, node)
  Input: the BST t and the node

  p = t.root
  if p=null do
      t.root=node
      return
  end
  while p≠null do
      prev=p
      if node.value<p.value do
          p=p.left
      else if node.value>p.value do
          p=p.rigℎt
      else
          return
  end
  if node.value<prev do
      prev.left=node
  else
      prev.rigℎt=node

find minimun

O(h)-ℎ is the depth of the tree

1
2
3
4
5
6
7
8
Algorithm Minimum(t)
  Input: the BST t

  p = t.root
  while p.left≠null do
      p=p.left
  end
  return p

Deletion in BST

  1. has no child

    delete the node

  2. has one child

    use the child to replace z

  3. has two children

    delete the minimum node x of the right subtree of z (i.e., x is the successor of z), then replace z by x.

    image-20230424233325065

Tree Traversal

Depth-first Tree Traversal

implement: stack
preorder 前序
1
2
3
4
5
def preorder(root):
    if not root: return 
    print(root.val)
    preorder(root.left)
    preorder(root.right)
postorder 后序
1
2
3
4
5
def postorder(root):
    if not root: return 
    preorder(root.left)
    preorder(root.right)
    print(root.val)
inorder 中序
1
2
3
4
5
6
def inorder(root):
    if not root: return 
    preorder(root.left)
    print(root.val)
    preorder(root.right)

Breadth-first Tree Traversal

implement: queue
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def bfs(root):
    if not roor: return
    q=[root]
    result=[]
    while q:
        child=[]
        for i in q:
            result.append(i)
            if i.left:
                child.append(i.left)
            if i.right:
                child.append(i.right)
        q=child
     return result

Sorting

stable, unstable, inplace, outplace

image-20230425140502996

Selection sort

image-20230425130213964
image-20230425130244294

time-\(O(n^2)\)

in-place

unstable

1
2
3
4
5
6
7
8
9
def selection_sort(arr):
	for i in range(len(arr)-1):
		min_ind = i
		for j in range(i+1, len(arr)):
            if arr[j]<arr[min_ind]:
                min_index=j
        if i!=min_ind:
            arr[min_ind],arr[i]=arr[i],arr[min_index]
    return arr

Insertion Sort

image-20230425130404747
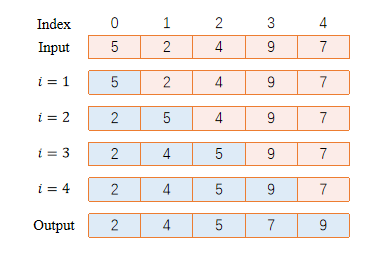
image-20230425130733053

time -\(O(n^2)\)

in-place

stable

1
2
3
4
5
6
7
8
def insertionSort(arr): 
    for i in range(1, len(arr)): 
        key = arr[i] 
        j = i-1
        while j >=0 and key < arr[j] : 
                arr[j+1] = arr[j] 
                j -= 1
        arr[j+1] = key

Merge Sort

time - O(nlogn)

not in-place

stable

  1. Divide: divide the array A into two sub-arrays (L and R) of n/2 numbers each.
  2. Conquer: sort two sub-arrays recursively.
  3. Combine: merge two sorted sub-arrays into a sorted array.
image-20230425141231598 
1
2
3
4
5
6
7
8
9
Algorithm MergeSort(A, n)
  Input: the n-size array A

  if n=1 then
      return A
  (L,R)=A
  L’=MergeSort(L)
  R’=MergeSort(R)
  return Merge(L’, R’)

Merge function - O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Algorithm Merge(A, n_A,B,n_B,C)
  Input: the n_A-size array A and n_B-size array B
  Output: the (n_A+n_B−1)-size array C

  i=0,j=0,k=0
  while i<n_A and j<n_B do
      if A[i]≤B[j] then
          C[k]=A[i], i=i+1
      else
          C[k]=B[j], j=j+1
      end
      k=k+1
  end
  if i=n_A then
      C[k,⋯]=B[j,⋯]
  else
      C[k,⋯]=A[i,⋯]
  end

Quick Sort

O(nlogn)

in-place