Regularization
.
什么是正则化
目的:防止模型过拟合
原理:正则化通过在损失函数中引入惩罚项来限制模型的复杂度,以防止模型过度拟合训练数据。惩罚项会在优化过程中对模型的参数进行调整,以平衡模型的拟合能力和泛化能力。
https://www.zhihu.com/question/20924039
最直接的防止过拟合的方法就是减少特征数量,就是减少0范数(向量中非零元素的个数),但是0范数很难求,所以就有了1范数,2范数。
作用:
- 防止过拟合
- 特征选择:l1正则化
- 改善模型稳定性
常见正则化
l1正则化
\[ l1=\lambda||\vec{w}||_1=\sum_i|w_i| \]
\(\lambda\)控制约束程度
l1不仅可以约束参数量,还可以使参数更稀疏。因为对目标函数经过优化后,一部分参数会变为0,另一部分参数为非零实值。非零实值说明这部分参数是最重要的特征。
假设参数分布是Laplace分布。
稀疏原因
https://blog.csdn.net/b876144622/article/details/81276818
https://www.zhihu.com/question/37096933/answer/70426653
0处导数突变,如果此时0+导数为正,优化时放负方向跑,0-导数为负数,优化时往正方向跑,就很容易落入0
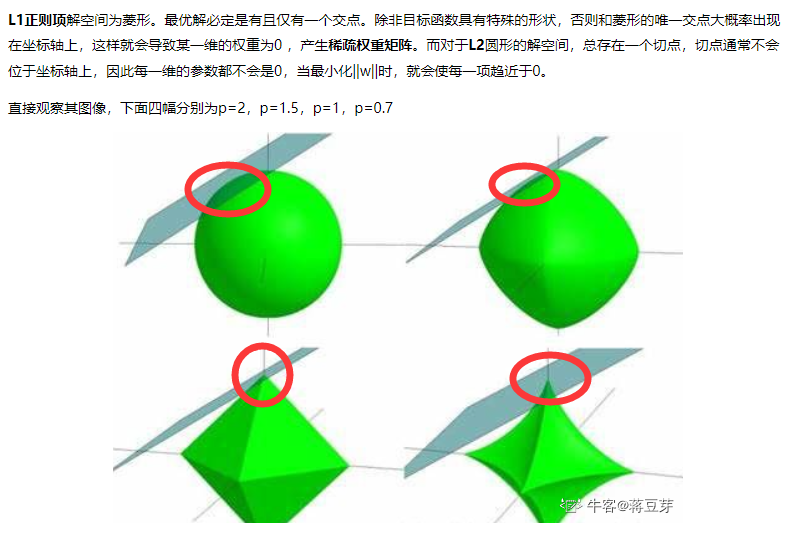
缺点
- 非光滑性:L1 正则化的正则化项是参数的绝对值之和,这导致目标函数在参数为零时不可导。这使得优化过程变得更加困难,特别是在使用梯度下降等基于梯度的优化算法时。在参数为零附近,梯度不连续,可能导致优化过程出现问题。
- 多重共线性:当特征之间存在高度相关性(多重共线性)时,L1 正则化倾向于选择其中一个特征,而忽略其他相关特征。这可能导致模型的解释性下降,因为被忽略的相关特征可能包含有用的信息。相比之下,L2 正则化对相关特征的惩罚更均衡,可以保留更多相关特征的权重。
- 不适用于高维问题:在高维问题中,特征数量远远大于样本数量时,L1 正则化可能不太适用。由于参数空间的维度过高,L1 正则化可能无法准确地选择特征,导致过拟合或选择不稳定的特征子集。
l2正则化
\[ l2=\frac{1}{2}\lambda||\vec{w}||_2^2=\sum_i|w_i|^2 \]
l2正则化会使部分特征趋近于0,也就达到正则化的目的了。
此外,l1正则化和l2正则化也可以联合使用,这种形式也被称为“Elastic网络正则化”。
假设参数分布是正态分布
Dropout
在训练的时候让一定量的神经元失活,在该epoch中不参与网络训练
dropout训练出的参数需要乘以keep-prib使用
因为神经元预测的时候就不应该随机丢弃,一种”补偿“的方案就是每个dropout训练出的神经元的权重都乘以一个p,这样在“总体上”使得测试数据和训练数据是大致一样的。保证测试的时候把这个神经元的权重乘以p可以得到同样的期望。比如一个神经元的输出是x,那么在训练的时候它有p的概率参与训练,(1-p)的概率丢弃,那么它输出的期望是。因此测试的时候把这个神经元的权重乘以p可以得到同样的期望。
注:目前主流是采用inverted dropout替代dropout,inverted dropout不需要乘以keep-prib。它的做法是在训练阶段对执行了dropout操作的层,其输出激活值要除以keep_prib,而测试的模型不用再做任何改动。除以(1-p),让期望与不dropout相同。
早停
每一个epoch训练结束后使用验证集验证模型效果,画出训练曲线,这样就可以判断是否过拟合了。当发现网络有点过拟合了,当然就是“早停”了,可以直接停止训练了。
扩充数据集
Augmentation,增加变化增加多样性
数据增强方法
数据集越大,网络泛化性能越好,所以努力扩充数据集,通过平移、翻转、旋转、放缩、随机截取、加噪声、色彩抖动等等方式。
BN(Batch Normalization)
目的:用于解决深度网络梯度消失和梯度爆炸的问题,加速网络收敛速度。
批规范化,即在模型每次随机梯度下降训练时,通过mini-batch来对每一层的输出做规范化操作,使得结果(各个维度)的均值为0,方差为1,然后在进行尺度变换和偏移。

m是mini-batch中的数据个数。前面的散步是对input数据进行白化操作(线性),最后的“尺度变换和偏移”操作是为了让BN能够在线性和非线性之间做一个权衡,而这个偏移的参数是神经网络在训练时学出来的。
经过BN操作,网络每一层的输出小值被“拉大”,大值被“缩小”,所以就有效避免了梯度消失和梯度爆炸。总而言之,BN是一个可学习、有参数(γ、β)的网络层。
尺度变换和偏移的作用:
归一会影响到本层网络A所学习到的特征(比如网络中间某一层学习到特征数据本身就分布在S型激活函数的两侧,如果强制把它给归一化处理、标准差也限制在了1,把数据变换成分布于s函数的中间部分,这样就相当于这一层网络所学习到的特征分布被搞坏了)
于是BN最后的“尺度变换和偏移”操作,让我们的网络可以学习恢复出原始网络所要学习的特征分布(衡量线性和非线性)
BN训练和测试有什么不同
训练时,均值和方差针对一个Batch。
测试时,均值和方差针对整个数据集而言。因此,在训练过程中除了正常的前向传播和反向求导之外,我们还要记录每一个Batch的均值和方差。
BN和LN的差别
LN:Layer Normalization,LN是“横”着来的,对一个样本,经过同一层的所有神经元做归一化。LN中同层神经元输入拥有相同的均值和方差,不同的输入样本有不同的均值和方差;LN不依赖于batch的大小和输入sequence的深度,因此可以用于batchsize为1和RNN中对边长的输入sequence的normalize操作。
BN:Batch Normalization,BN是“竖”着来的,经过一个神经元的所有样本做归一化,所以与batch size有关系。
二者提出的目的都是为了加快模型收敛,减少训练时间。
如何同时使用BN和dropout
同时使用BN和Dropout会出现方差偏移的现象,原因:
使用Dropout:训练的时候以概率p drop了一些节点,比如dropout设置为0.5,隐藏层共有6个节点,那训练的时候有3个节点的值被丢弃,而测试的时候这6个节点都被保留下来,这就导致了训练和测试的时候以该层节点为输入的下一层的神经网络节点获取的期望会有量级上的差异。为了解决这个问题,在训练时对当前dropout层的输出数据除以(1-p),之后再输入到下一层的神经元节点,以作为失活神经元的补偿,以使得在训练时和测试时每一层的输入有大致相同的期望。
但是这样使得神经元输入期望大致相同,但是方差不一样,而BN是通过均值方差计算的,所以会导致输出不正确。
解决方法:
- 只在所有BN层的后面采用dropout层。
- dropout原文提出了一种高斯dropout,论文再进一步对高斯dropout进行扩展,提出了一个均匀分布Dropout,这样做带来了一个好处就是这个形式的Dropout(又称为“Uout”)对方差的偏移的敏感度降低了
Bagging 和Bootstrap?
Bootstrap是一种抽样方法,即随机抽取数据并将其放回。如一次抽取一个样本,然后放回样本集中,下次可能再抽取这个样本。接着将每轮未抽取的数据合并形成袋外数据集(Out of Bag, OOB),用于模型中的测试集。
Bagging算法使用Bootstrap方法从原始样本集中随机抽取样本。共提取K个轮次,得到K个独立的训练集,元素可以重复。用K个训练集训练K个模型。分类问题以结果中的多个值投票作为最终结果,回归问题以平均值作为最终结果。结果采用投票法,避免了决策树的过拟合问题。
Boosting是为每个训练样本设置一个权重,在下一轮分类中,误分类的样本权重较大,即每轮样本相同,但样本权重不同;对于分类器来说,分类误差小的分类器权重较大,反之则小。
采用模型融合的方式也可以避免过拟合。
参数共享
参数共享是一种在神经网络中常用的正则化方法,特别适用于卷积神经网络(CNN)。通过在神经网络的不同层之间共享参数,可以减少模型的参数数量,提高模型的效率和泛化能力。
数据标准化
数据标准化是对数据进行预处理的一种方式,将数据按特征进行缩放,使得每个特征的均值为 0,标准差为 1。这有助于使不同特征之间的尺度一致,提高模型的收敛速度和性能。
- z-score
- min-max