王树森推荐系统公开课

Posted on 2023-03-13 Edited on 2024-06-19 In RecSys , BasicTurtorial

基本概念

指标

消费指标

点击率=点击次数/曝光次数

点赞量=点赞次数/点击次数

收藏率=收藏次数/点击次数

转发率=转发次数/点击次数

阅读完成率=滑动到底次数/点击次数$\times f(笔记长度)$

北极星指标

用户规模：日活用户数（DAU），月活用户数（MAU）

消费：人均使用推荐时长、人均阅读笔记数量

发布：发布渗透率、人均发布量

AB测试

完成离线测试后，使用线上小流量AB测试考察指标，或者用AB测试调参（GNN深度）

随机分桶

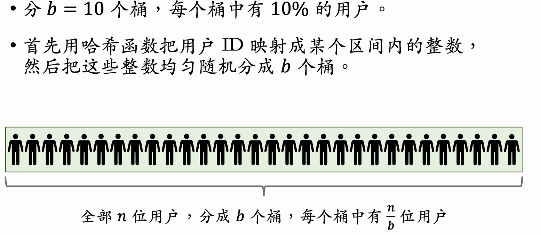
在不同的桶上使用不同的策略或参数实验。

分层实验

不同的部门都需要做AB测试，每个部门对应一个层，分层实验满足：

同层互斥：同一个部门做实验不能使用同一个桶；例：GNN实验占了召回层4个桶，其它召回实验只能用剩下的6个桶。
不同层正交：每一层独立随机对用户做分桶。每一层都可以独立用100%的用户做实验。

召回

协同过滤

基于物品的协同过滤 ItemCF

基本思想：如果用户喜欢item1,而item1与item2相似，那么用户很可能喜欢item2.

基本结构：

我们从用户历史互动知道用户对$item_j$，感兴趣利用下面公式计算对候选物品的兴趣分数 \[ \sum_jlike(user,item_j)\times sim(item_j,item) \] 在这个例子中，用户对候选item的兴趣是：$2\times 0.1+1\times0.4+4\times0.2+3\times0.6=3.2$,我们计算所有item的分数，然后返回分数最高的若干个item

计算item相似度

可以通过与item交互过的用户重合度计算item相似度（其中一种方法，也可以用KG）

方法1：不考虑用户对物品的喜欢程度

\[ sim(i_1,i_2) = \frac{|W1 \cap W2|}{\sqrt[2]{|W1|\cdot |W2|}} \]

其中，喜欢物品$i_1$的用户记作$W_1$,喜欢物品$i_2$的用户记作$W_2$.

方法2：考虑用户对物品的喜欢程度,使用余弦相似度！

把每个item用向量表示 \[ i_1=[like(u_1,i_1),like(u_2,i_1),\cdots ,like(u_n,i_1)] \space u_n\in W \]

\[ i_2=[like(u_1,i_2),like(u_2,i_2),\cdots ,like(u_n,i_2)] \space u_n\in W \]

\[ W=W_1\cup W_2 \]

我们使用余弦相似度计算： \[ similarity=cos(\theta) = \frac{A\cdot B}{||A||\space ||B||} \] 如果有用户k只喜欢其中一个物品:只喜欢$i_1$不喜欢$i_2$,那么$i_2[k]=0$，所以点乘后第k项为0，所以点乘只与同时喜欢$i_1,i_2$的用户有关系，如下面公式 \[ sim(i_1,i_2) = \frac{\sum_{v\in V}like(v,i_i)\cdot like(v,i_2)}{\sqrt[2]{\sum_{u_1\in W_1}like^2(u_1,i_1)}\sqrt[2]{\sum_{u_2\in W_2}like^2(u_2,i_2)}} \]
皮尔逊系数 \[ sim(i,j)=\frac{\sum_{p\in P}(R_{i,p}-\bar R_i)(R_{j,p}-\bar R_j)}{\sqrt{\sum_{p\in P}(R_{i,p}-\bar R_i)^2}\sqrt{\sum_{p\in P}(R_{j,p}-\bar R_j)^2}} \]

运作基本流程

实现做离线计算，预先计算两个索引：

“user2item”：记录每个用户最近点击交互过的n个物品ID（lastN）

# example 不一定是公司真实的保存方式
user2item={
    'u1':[[i1,like(u1,i1)],[i2,like(u1,i2)],...,[in,like(u1,in)]]
    ...
}

"item2item":计算物品之间两两相似度，记录每个物品最相似的k个物品。

item2item={
	#target item:[[similar item, similarity score]...]
	'i1':[[i2,0.9],[i6,0.88]...]
	'i2':...
}

线上做召回
1. 给定用户ID，通过“user2item”找到用户近期感兴趣的物品列表(last-n)
2. 对于last-n列表中每个物品，通过“item2item"找到top-k相似物品。现在有1个user，n个互动物品，nxk个候选物品。
3. 计算候选物品兴趣分数
4. 返回分数最高的100个物品作为推荐结果

Swing召回通道

如果两个Item的重合用户来源于一个小圈子（微信群），一个小圈子用户同时与两个Item交互，不能说明两个Item相似，如果很多不相关的用户交互两个Item，说明Item相似。

基本结构

计算用户重合度

用户\[u_1\]喜欢的物品记作集合\[J_1\]

用户\[u_2\]喜欢的物品记作集合\[J_2\]

定义两个用户的重合度： \[ overlap(u_1,u_2)=|J_1\cap J_2| \] 用户\[u_1\]和\[u_2\]的重合度高，则他们可能来自一个小圈子，要降低他们的权重。

计算物品相似度

喜欢物品\[i_1\]的用户记作集合\[W_1\]

喜欢物品\[i_2\]的用户记作集合\[W_2\] \[ V=W_1\cap W_2 \]

\[ sim(i_1,i_2) = \sum_{u_1\in V}\sum_{u_2\in V}\frac{1}{\alpha+overlap(u_1,u_2)} \]

u1u2都对物品i1i2感兴趣，这样的用户越多，说明物品越相似

\[\alpha\]是超参数

基于用户的协同过滤（UserCF）

假设：u1与u2兴趣十分相似，u1可能会对u2交互的item感兴趣

何为兴趣相似：

点击、点赞、收藏、转发的笔记有很大重合
关注的作者有很大的重合

基本结构

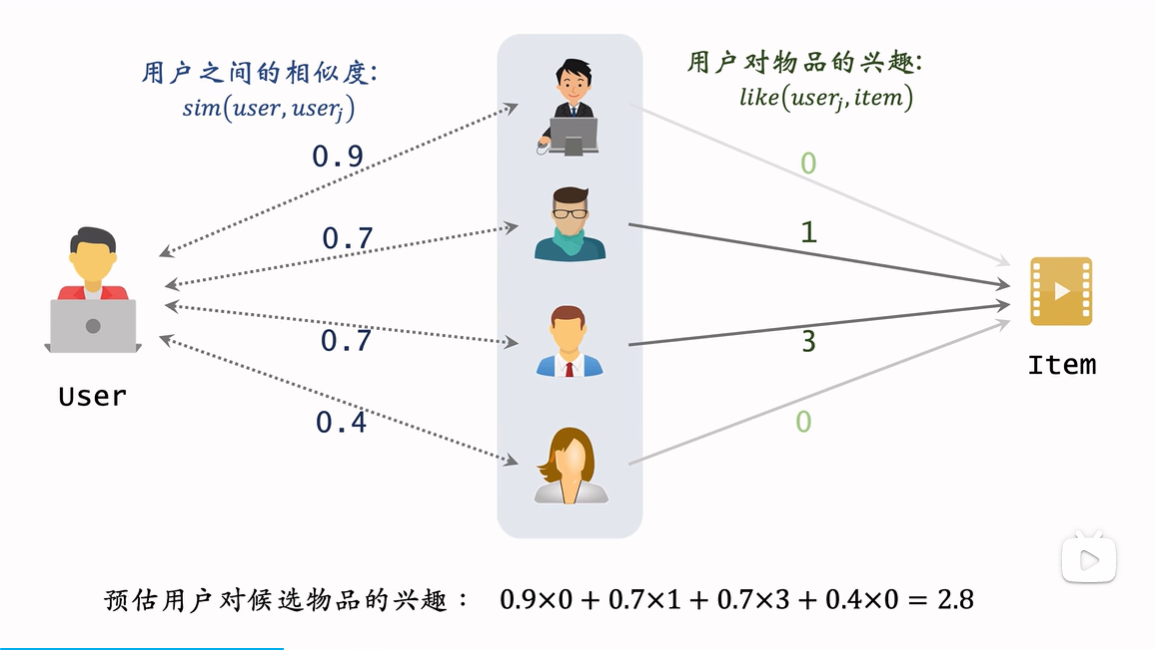\[ \sum_jsim(user,user_j)\times like(user_j,item) \]

计算User相似度

计算User相似度

把每个用户表示为一个稀疏向量，向量每个元素对应一个物品。相似度sim就是两个向量夹角的余弦。\[u_1\cdot u_2\]结果就是\[|I|\]

\[ sim(u_1,u_2) = \frac{|I|}{\sqrt{|J_1|\cdot|J_2|}} \]

\[J_1\]: 用户\[u_1\]喜欢的物品集合

\[J_2\]: 用户\[u_2\]喜欢的物品集合

\[I\]：\[J_1\cap J_2\]

|*|:集合的大小

\[sim(u_1,u_2)\in[0,1]\],越大代表用户越相似

降低热门物品权重

大家都喜欢哈利波特，哈利波特对用户相似度计算意义小,所以我们降低热门物品权重 \[ sim(u_1,u_2) = \frac{\sum_{l\in I}weight(l)}{\sqrt{|J_1|\cdot|J_2|}} \]

\[ weight(l) = \frac{1}{log(1+n_l)} \]

\[n_l\]: 喜欢物品l的用户数量，反应物品的热门程度。\[n_l\]越大，\[log(1+n_l)\]越大，权重越小

运作基本流程

实现做离线计算，预先计算两个索引：

“user2item”：记录每个用户最近点击交互过的n个物品ID（lastN）

# example 不一定是公司真实的保存方式
user2item={
    'u1':[[i1,like(u1,i1)],[i2,like(u1,i2)],...,[in,like(u1,in)]]
    ...
}

"user2user":计算用户之间两两相似度，记录每个用户最相似的k个用户。

user2user={
	#target user:[[similar user, similarity score]...]
	'u1':[[u2,0.9],[u6,0.88]...]
	'u2':...
}

线上做召回
1. 给定用户ID，通过“user2user”找到top-k相似用户
2. 对于top-k列表中每个用户，通过“user2item"找到用户近期感兴趣物品列表(last-n)。
3. 对于召回的nk个相似物品，用公式预估用户对每个物品的兴趣分数
4. 返回分数最高的100个物品，作为召回结果

协同过滤缺点

。。。

向量召回

矩阵补充 Matrix Completion

用于填充评分矩阵中无评分的部分，通过求user与item embedding的内积

数据集

（用户ID,物品ID，兴趣分数）————》$dataset={(u,i,y)}$
正负例子（0-4分）：
1. 负例子：曝光没有点击-0分
2. 正例子：点击、点赞、收藏、转发-各1分

训练

\[ min_{A,B}\sum _{(u,i,y)\in dataset}(y-<a_u,b_i>)^2 \]

缺点

仅用ID embedding，没利用物品、用户的属性。
负样本选取方法不对。
做训练方法不好
1. 内积效果不如余弦相似度
2. 用回归方法不如用分类方法。

运作基本流程

离线计算
1. 训练矩阵A、B（embedding层的参数，A for user, B for item）
2. 由于矩阵很大，为了快速读取使用hash方法：
  1. 把矩阵A存储到key-value表{user_id: user_embedding}。
  2. （加速最近邻查找）将item分区保存至key-value表
线上服务
1. 通过用户ID查询用户向量，记作A。
2. 最近邻查找：查找用户最优可能感兴趣的k个物品作为召回结果。
  1. 第i号物品的embedding向量记作$b_i$
  2. 求$<a,b_i>$
  3. 返回内积最大的k个物品

加速最近邻查找方法：

一般item有几亿个，暴力计算内积并排序过慢

方法：

确定衡量最近邻标注：欧氏距离最小（L2距离），向量内积最大（内积相似度），向量夹角余弦最大（cosine相似度）
根据衡量标准将所有item embedding分块，下面为根据余弦相似度分块的例子，每一个区域用一个向量E表示，通过key-value表保存区域向量E与区域中所有向量的embedding。
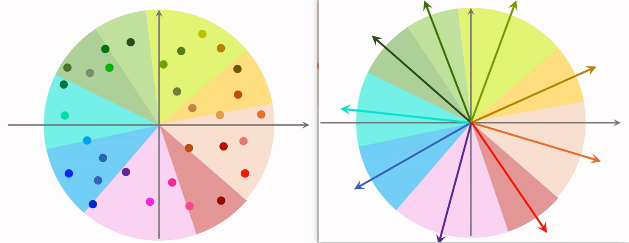
求区域向量与user的余弦相似度，获取结构最大区域。再将区域中所有的item暴力枚举算相似度。

双塔模型

融合除了ID以为的别的特征

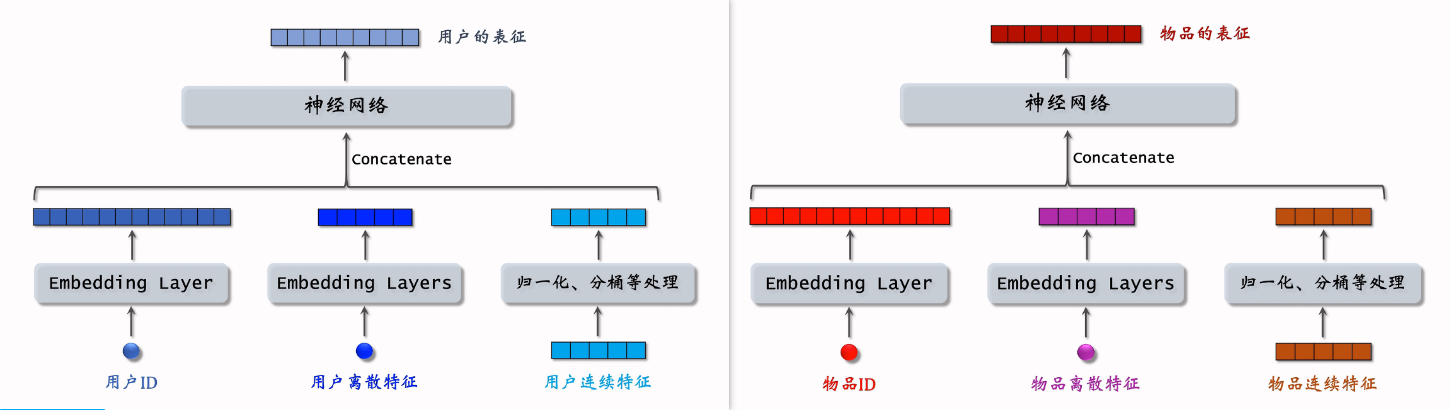
数据集

正样本

曝光且有点击的（user，item）组

问题：少部分物品占据大部分点击，导致正样品大多是热门物品，对冷门物品不公平。

解决：过采样冷门物品，或降采样热门物品

过采样：一个样品出现多次

降采样：一些样本被抛弃
负样本

混合几种负样本：50%的简单负样本，50%的困难负样本

我们分别讨论下面三种可以作为负样本的数据。
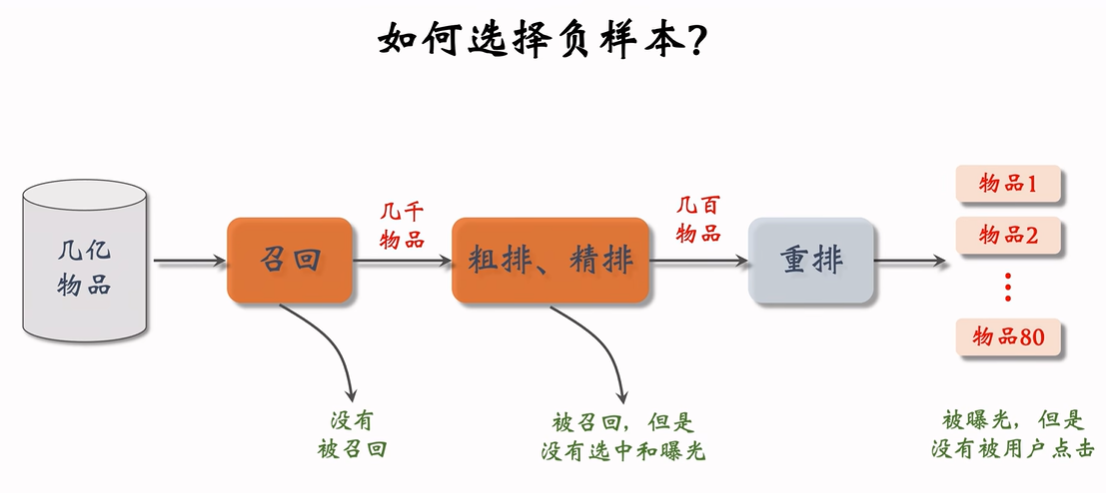
1. 简单负样本
  
  没有被召回的数据: 全体物品
  
  没被召回的数据，大概率是用户不感兴趣的，未被召回的样本约等于全体物品，所以在全体物品中做抽样作为负样本。
  
  均匀抽样：正样本大多是热门物品，负样本大多是冷门物品。（因为热门物品比例小），所以我们需要利用非均匀抽样打压热门物品。
  
  非均抽采样：负样本抽样概率与热门程度（点击次数）正相关，$抽样概率\propto (点击次数)^{0.75}$
  
  Batch内负采样
  
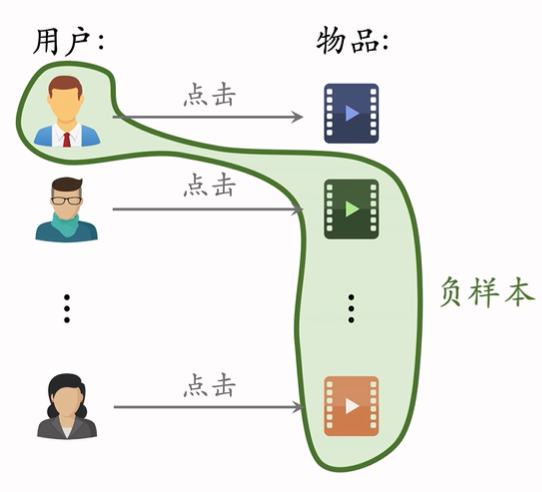
  一个batch有n个正样本对，一个用户和n-1个物品组成负样本，batch中一共有n（n-1）个负样本对。
  
  此时，热门物品成为负样本的概率过大（热门物品成为正样本概率大）：$抽样概率\propto (点击次数)$
  
  所以做训练时，兴趣分数调整为：$cos(a,b_i)-logp_i$降低热门物品作为负样本的惩罚
2. 困难负样本：用户有一点兴趣，但兴趣不够，特别容易分错
  
  被粗排淘汰的物品（比较困难）
  
  精排分数靠后的物品（非常困难）
注意：不能用曝光但没有点击的样本，因为能通过精排（更复杂的模型）的样本已经是用户比较感兴趣的样本，可能只是机缘巧合没有点击，训练召回不能用这一类样本，但是训练排序可以

训练

Pointwise

当做二分类任务，对于正样本，鼓励cos(a,b)接近+1；对于负样本，鼓励cos(a,b)接近-1

Pairwise

鼓励$cos(a,b^+)$大于$cos(a,b^-)$

Triplet hinge loss: \[ L(a,b^+,b^-) = max\{0,cos(a,b^-)+m-cos(a,b^+)\} \] m为超参数

Triplet logistic loss: \[ L(a,b^+,b^-) = log(1+exp[\sigma(cos(a,b^-)-cos(a,b^+))]) \]

Listwise

运作基本流程

离线存储：把物品向量b存入向量数据库。
线上召回：查找用户最感兴趣的k个物品。
1. 给定用户ID和画像，线上用升级网络算用户向量A。
2. 最近邻查找

为什么用户向量要在线计算：

没做一次召回只用到一个用户向量A，计算成本较小。
用户兴趣动态变化，物品较稳定。

模型更新

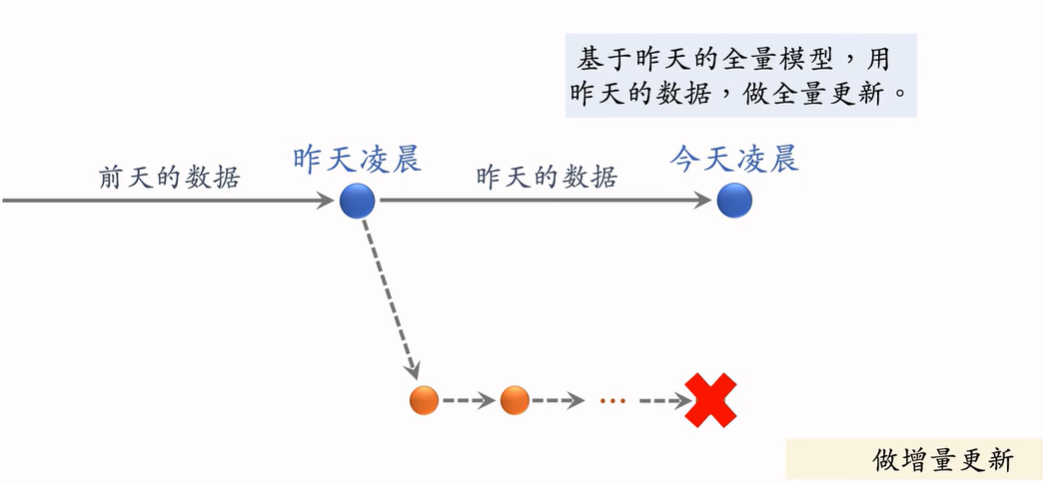
全量更新：

在昨天模型参数基础上做训练（不是随机初始化），用昨天的数据，shuffle后训练一个epoch后发布新的用户塔神经网络和物品向量，供线上召回使用。

增量更新：

用户兴趣随时发生变化，实时收集线上数据，对模型做online learning，增量更新ID Embedding参数(不更新神经网络其他部分参数)，发布用户ID Embedding，供用户塔线上计算用户向量。

不能只做增量更新，不做全量更新

小时级数据有偏差，分钟级偏差更大。
全量更新：random shuffle一天数据，做 1epoch训练；增量更新按照数据从早到晚顺序做1epoch训练，全量更新效果更好。

自监督学习

背景

推荐系统头部效应严重：少部分物品占据大部分点击，大部分物品曝光、点击次数不高，导致高点击物品的表征学习的好，长尾物品的表征学的不好，用自监督学习做data augmentation，更好的学习长尾物品的向量表征。

Method

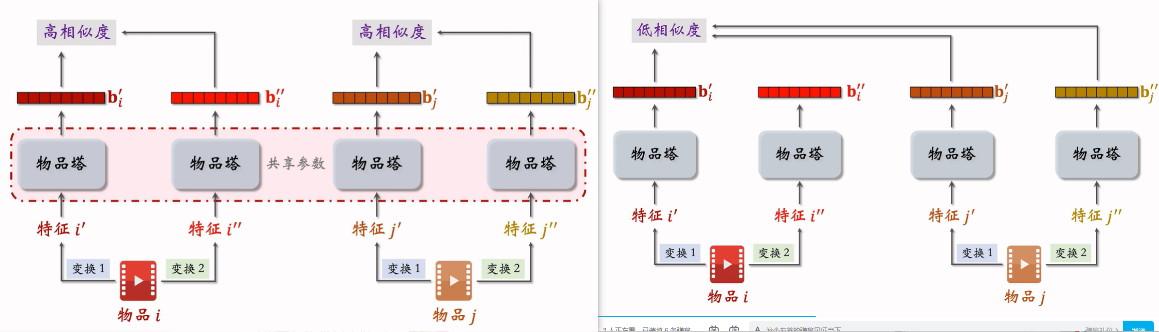
特征变换方法

Random Mask

随机选一些离散特征(例如类目特征)，把它们遮住

例子：$U=\{数码，摄影\}$->$U'-\{default\}$
Dropout

一个物品可以有多个类目，那么类目是一个多值离散特征。Dropout会随机丢弃特征中50%的值。

例子：$U=\{数码，摄影\}$->$U'-\{数码\}$
complementary互补特征

假设物品一共有四种特征：ID,类目，关键词，城市

随机分成两组：{ID,关键词}，{类目，城市}

{ID,default，关键词，default}作为表征i‘

{default，类目，default，城市}作为表征i‘’
Mask一组关联的特征

p(u): 某特征取值为u的概率

p(u,v):某特征取值为u，另一个特征取值为v同时发生的概率

离线计算特征的两两关系，用户信息(mutual information): \[ MI(U,V)=\sum_{u\in U}\sum_{v\in V}p(u,v)\cdot log\frac{p(u,v)}{p(u)\cdot p(v)} \] 假设一共有k种特征。离线计算两两MI，得到kxk的矩阵，随机选一个特征为种子，找到种子最相关的k/2中特征Mask掉，保留其余的k/2中特征。

比random mask、dropout、互补特征等方法效果更好，但方法复杂实现难度大不容易维护。

自监督训练

从全体物品中均匀抽样得到m个物品，作为一个batch。

做两类特征变换，物品他输出两组向量。

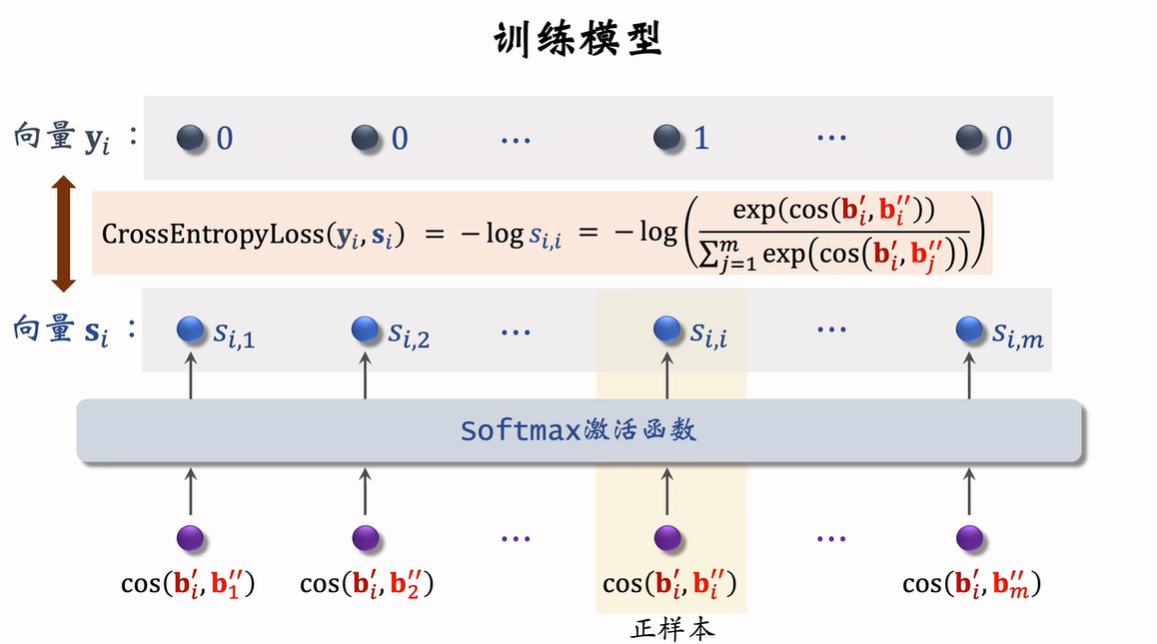
自监督训练+正常训练

不适合召回的模型

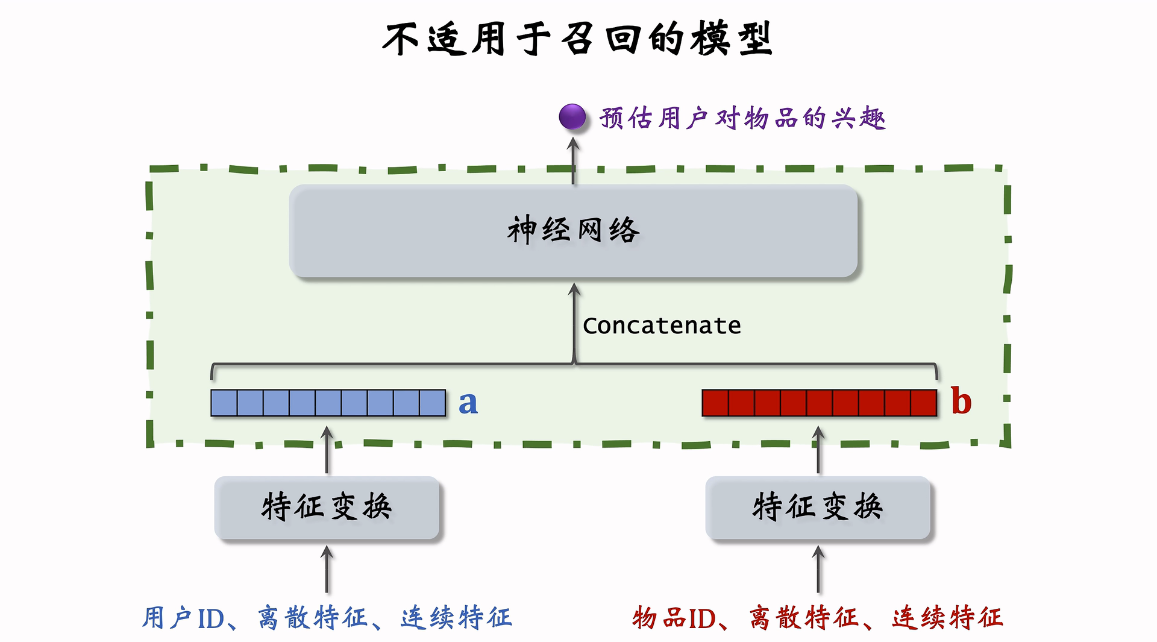
召回需要计算的item量很大，所以我们一般只做后期融合（计算相似度的时候再融合user和item的embedding），因为融合步骤一般要在线计算不能离线计算完保存（需求内存量太大）。如果我们在召回阶段就要让user embedding与上亿个item embedding过神经网络模型，这样时间复杂度太高了。

其他方式召回

地理召回

作者召回

缓存召回：复用前n次推荐精排的结果

曝光过滤与链路

如果用户看过某个物品，则不再把该物品曝光给该用户
对于每个用户，记录已经曝光给他的物品。(小红书只召回1个月以内的笔记，因此只需要记录每个用户最近1个月的曝光历史。)
对于每个召回的物品，判断它是否已经给该用户曝光过排除掉曾经曝光过的物品。
一位用户看过n个物品，本次召回r个物品，如果暴力对比，需要O(nr)的时间。

Bloom Filter

Bloom filter 判断一个物品ID是否在已曝光的物品集合中。
如果判断为no，那么该物品一定不在集合中
如果判断为yes，那么该物品很可能在集合中。(可能误伤错误判断未曝光物品为已曝光，将其过滤掉)
Bloom flter 把物品集合表征为一个m维二进制向量。
Bloom filter有k个哈希函数，每个哈希函数把物品I映射成介于0和m-1之间的整数。
已曝光物品和召回物品都可以用这个m维向量表示。

当k=1：

当k=3：

BloomFilter误伤概率：

曝光物品集合大小为n，二进制向量维度为m，使用k个哈希函数。
误伤的概率为$δ≈(1-exp(-\frac{kn}{m}))^k$
- n越大，向量中的1越多，误伤概率越大。
- m越大，向量越长，越不容易发生哈希碰撞。但要求更多存储空间。
- k太大、太小都不好，k有最优取值。
计算k最优参数，设定可容忍误伤概率$δ$：
$k=1.44\cdot ln(\frac{1}{δ})$
$m=2n\cdot ln(\frac{1}{δ})$

优缺点

Bloom filtcr 把物品的集合表示成一个二进制向量，节省存储空间和计算成本。
每往集合中添加一个物品，只需要把向量k个位置的元素置为1。(如果原本就是1，则不变)
Bloom filter只支持添加物品，不支持删除物品。
每天都需要从物品集合中移除年龄大于1个月的物品(超龄物品不可能被召回，没必要把它们记录在Bloom filter，降低n可以降低误伤率)

排序

排序模型特征

用户画像

用户ID
性别、年龄
新老、活跃度
感兴趣类目、关键词、品牌

物品画像

物品ID
发布时间
GeoHash（经纬度编码）、所在城市
标题、类目、关键词、品牌
字数、图片数、视频清晰度、标签数
内容信息量、图片美学

用户统计特征

用户最近30天天曝光数、点击数、点赞数、收藏数
按照笔记图文/视频分桶。(比如最近7天，该用户对图文笔记的点击率、对视频笔记的点击率。)
按照笔记类目分桶。(比如最近30天，用户对美妆笔记的点击率、对美食笔记的点击率、对科技数码笔记的点击率。)

笔记统计特征

笔记最近30天(7天、1天、1小时)的曝光数、点击数点赞数、收藏数…。
按照用户性别分桶、按照用户年龄分桶…
作者特征:
- 发布笔记数
- 粉丝数
- 消费指标(曝光数、点击数、点赞数、收藏数)

场景特征

用户定位GeoHash(经纬度编码)、城市。
当前时刻(分段，做embedding)
是否是周末、是否是节假日。
手机品牌、手机型号、操作系统。

特征处理

离散特征:做embedding。
- 用户ID、笔记ID、作者ID。
- 类目、关键词、城市、手机品牌
连续特征:做分桶，变成离散特征。
- 年龄、笔记字数、视频长度。
- 连续特征:其他变换。
- 曝光数、点击数、点赞数等数值做log(1+x)
- 转化为点击率、点赞率等值，并做平滑。

粗排模型

给几千篇笔记打分
单次推理代价必须小（用户与物品特征后期融合）
预估的准确性不高

粗排的三塔模型

精排模型

给几百篇笔记打分
单次推理代价很大（用户与物品特征前期融合）
预估准确性更高

多目标模型

模型结构

loss： \[ Loss=\sum_{i=1}^4\alpha_i \cdot CrossEntropy(y_i,p_i) \]

估值校准：

why：为了缩短训练时间会对负样本进行降采样，由于负样本变少，预估点击率大于真实点击率：

真实点击率:$p_{true}=\frac{n_+}{n_++n_-}$

预估点击率：$p_{pred}=\frac{n_+}{n_++\alpha \cdot n_-}$

校准公式： $p_{true}=\frac{\alpha \cdot p_{pred} }{(1-p_{pred})+\alpha \cdot p_{pred}}$

Multi-gate Mixture-of-Experts (MMoE)

模型结构

假设现在需要求点击率与点赞率两个指标

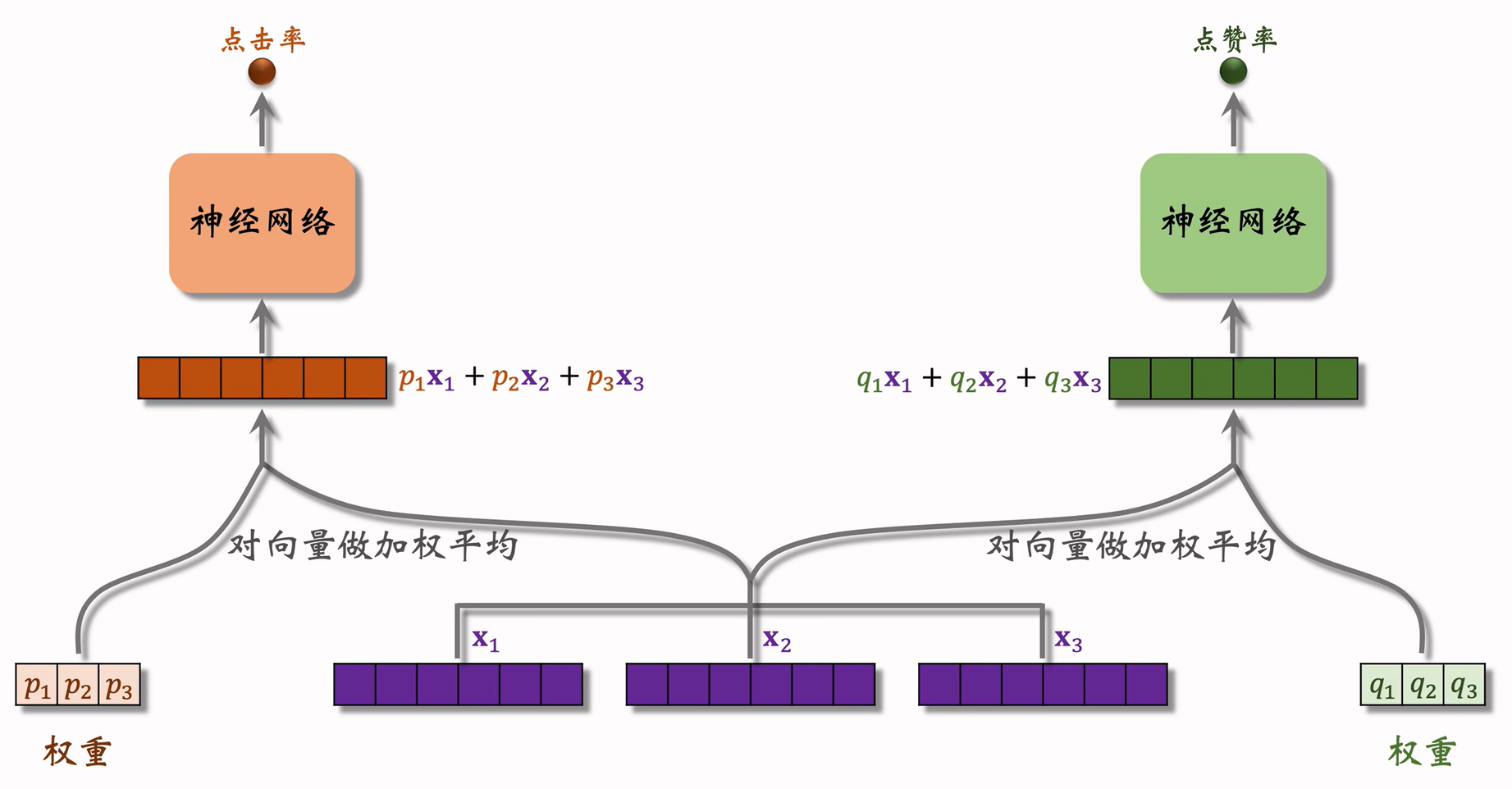
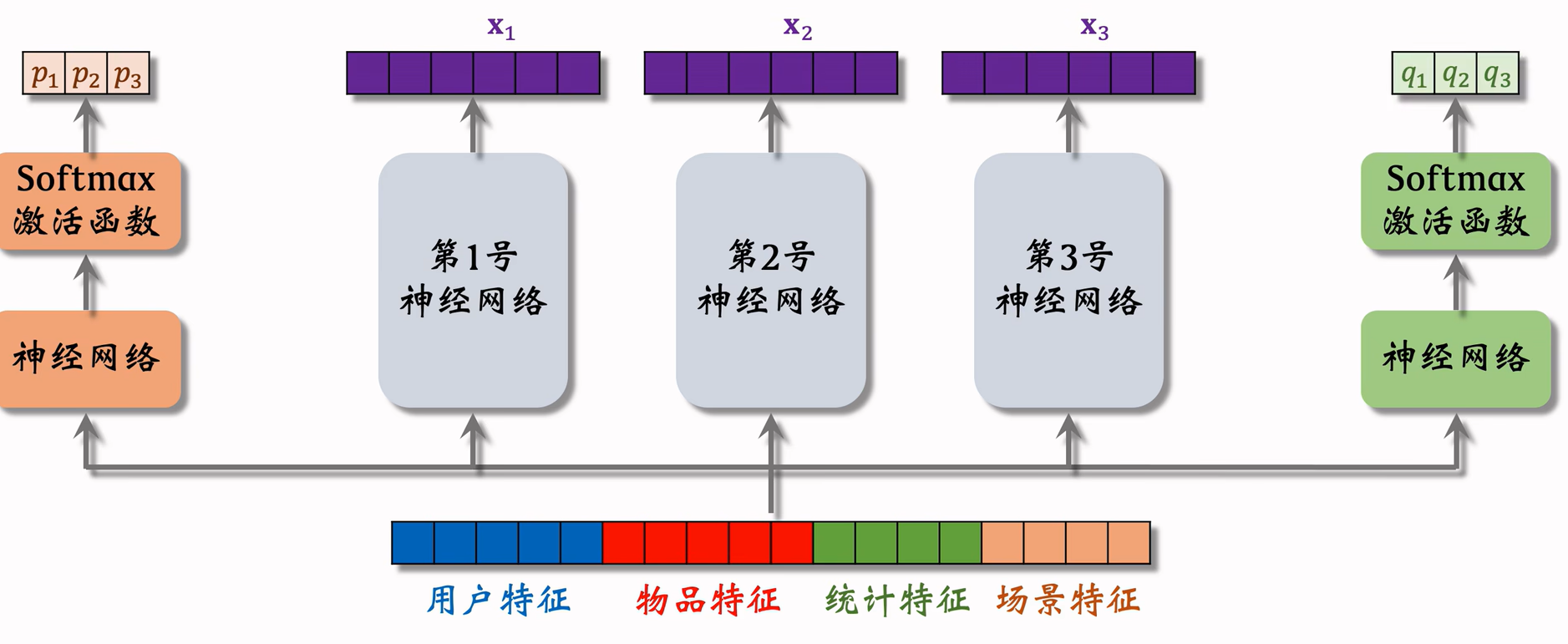
极化现象

softmax输出的权重接近与0,0,0...1，这样不能充分利用所有模型结构

解决方法：dropout

预估分数融合

将点击率、点赞量等指标融合，计算出最终分数

简单加权和

$p_{click}+w_1\cdot p_{like}+ w_2\cdot p_{collect} + \cdots$
点击率乘以其他项加权和

$p_{click}\cdot (w_1\cdot p_{like}+ w_2\cdot p_{collect} + \cdots)$
海外某短视频app：

$(1+w_1\cdot p_{time})^{\alpha_1}\cdot (1+w_2\cdot p_{time})^{\alpha_2}\cdots$

$p_{time}$是预估播放时长
国内某视频app：用排名计算
电商

视频播放时长建模

播放时长建模

训练：最小化y与p的交叉熵函数

预测：直接求$exp(z)$

视频完播

建模方法

回归方法

视频长度10分钟，实际播放4分钟，则实际播放率为y=0.4 让预估播放率p拟合y: $loss=y·logp+(1-y)·log(1-p)$

线上预估完播率，模型输出p=0.73，意思是预计播放73%。
二元分类

定义完播指标，比如完播80%。例:视频长度10分钟，播放$>$8分钟作为正样本，播放$<$8分钟作为负样本。做二元分类训练模型:播放$>$80%vs 播放$<$80%。线上预估完播率，模型输出p=0.73，意思是P(播放>80%)= 0.73

融入融分公式

不可直接使用融分公式，因为视频越长完播率越低

需要做调整: \[ p_{finish}=\frac{预估完播率}{f（视频时长）} \] "把$p_{finish}$作为融分公式中的一项。

特征交叉

Factorized Machine

tbd

DCN

使用场景：

双塔模型中用户塔和物品塔
排序模型
MMOE模型中专家网络

PPNet

语音识别中的LHUC

PPNET

SENet

有点像autoencoder+全局注意力机制，中间缩小参数量m/r是避免过拟合

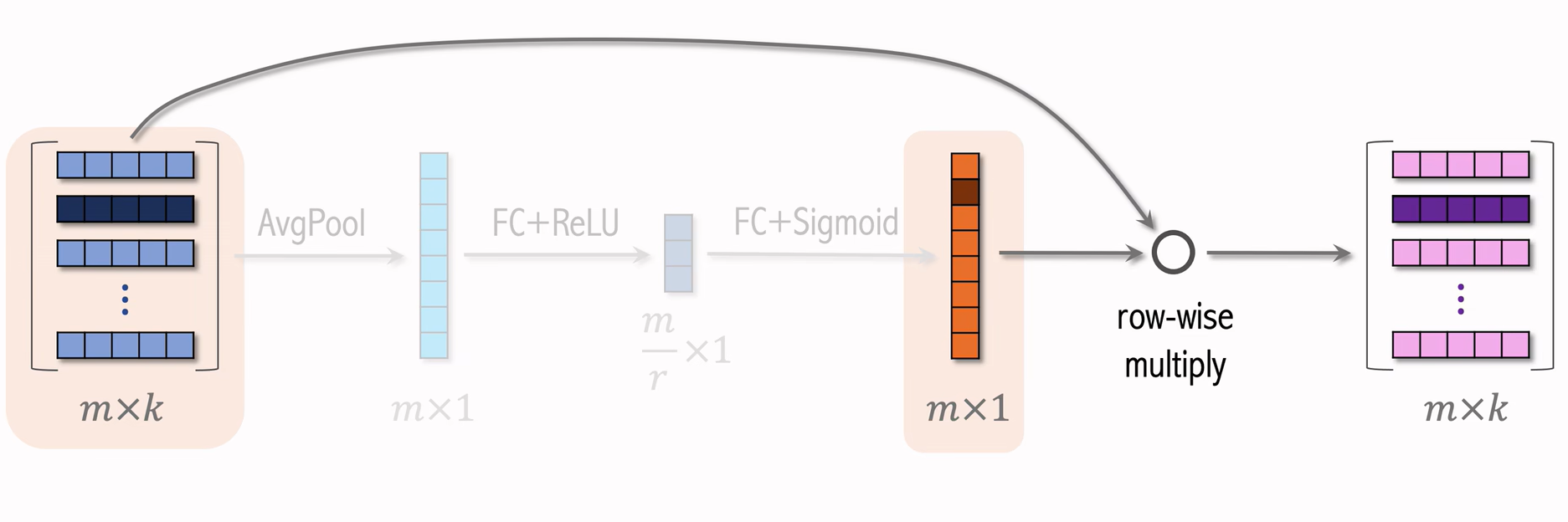
bilinear cross

内积 bilinear cross

哈达玛bilinear cross

FiBiNet

用户行为序列建模

Last N

用户最近的n次交互(点击、点赞等)的物品 ID。
对Last N物品I做embedding，得到n个向量。
把几个向量取平均，作为用户的一种特征。

DIN模型（注意力机制）

对于某候选物品，计算它与用户 Last N物品的相似度。
以相似度为权重，求用户Last N物品向量的加权和，结果是一个向量。
把得到的向量作为一种用户特征，输入排序模型，预估(用户，候选物品)的点击率、点赞率等指标。

简单平均和注意力机制都适用于精排模型。

简单平均适用于双塔模型、三塔模型。
- 简单平均只需要用到LastN，属于用户自身的特征。
- 把LastN向量的平均作为用户塔的输入。
注意力机制不适用于双塔模型、三塔模型。
- 注意力机制需要用到LastN+候选物品。
- 用户塔看不到候选物品，不能把注意力机制用在用户塔

SIM模型（长序列建模）

DIN模型缺点：

注意力层计算量与n相关
只能记录最近几百个物品，否则计算量太大
关注短期兴趣，遗忘长期兴趣

SIM模型目的：

保留用户长期行为序列，而且计算量不会很大。

改善DIN方法：DIN对Last N向量做加权平均，权重是相似度，如果某Last N物品与候选物品差异很大，则权重接近零。可以提前快速排除掉与候选物品无关（相似度低，权重接近0）的Last N物品，降低注意力层的计算量。

模型架构

保留用户长期行为记录，n的大小可以是几千。
对于每个候选物品，在用户Last N记录中做快速查找，找到k个相似物品。
把LastN变成TopK，然后输入到注意力层
SIM 模型减小计算量(从n降到k)。

查找

Hard Search（基于规则）
- 根据候选物品的类目，保留Last N物品中类目相同的。 ·简单，快速，无需训练。
Soft Search
- 把物品做embedding，变成向量。
- 把候选物品向量作为query，做k近邻查找，保留LastN物品中最接近的k个。
- 效果更好，编程实现更复杂。

注意力机制

只使用挑出来的Top K计算权重
使用时间信息：SIM序列长，记录用户长期行为，时间越久远，重要性越低
- 用户与某个LastN物品的交互时刻距今为δ。
- 对δ做离散化，再做embedding，变成向量d
- 把两个向量做concatenation，表征一个LastN物品。
  - 向量x是物品embedding。
  - 向量d是时间的embedding

重排

粗排精排：

粗排和精排用多目标模型对物品做 pointwise打分。
对于物品i，模型输出点击率、交互率的预估，融合成分数reward。$reward_i$表示用户对物品i的兴趣，即物品本身价值。

后处理（精排的后处理称为重排）：

从n个后序物品选出k个，既要她们总分高，也需要它们有多样性

相似性度量

提高多样性意味着推荐的物品不可过于相似，首先需要度量物品之间相似度

基于物品属性标签。

物品属性标签：类目、品牌、关键词………

根据一级类目、二级类目、品牌计算相似度

物品i:美妆、彩妆、香奈儿
物品j:美妆、香水、香奈儿

相似度:simi(i,j)=1，simz(i,j)=0，sim3(i,j)=1。在做加权

基于物品向量表征。

用召回的双塔模型学到的物品向量(不好)

召回双塔模型基于用户物品交互，冷门物品没办法学好表征，热门物品多交互也不代表相似
基于内容的向量表征(好)

用cv或nlp模型，提取特征

使用clip预训练方法：对于图片文字二元组，预测图文是否匹配，无需人工标注

Maximal Margianl Relevance（MMR）

精排给n个候选物品打分，把第i和j个物品的相似度记作 sim(i,j)，从几个物品中选出k个，既要有高精排分数也要有多样性。

原理

流程

1.已选中的物品S初始化为空集，未选中的物品初始化为全集 {1,…,n} 2.选择精排分数rewardi最高的物品，从集合R移到S 3.做k-1轮循环: a.计算集合见中所有物品的分数$\{MR_i\}_{i\in R}$。 b.选出分数最高的物品，将其从$R$移到$S$。

Trick：滑动窗口

已选中的物品越多(即集合S越大)，越难找出物品$i\in R$使得i与S中的物品都不相似。
设sim 的取值范围是「0,1]。当S很大时，多样性分数${max}_{j\in S}sim(i,j)$总是约等于1,导致 MMR 算法失效。
解决方案:设置一个滑动窗口W，比如最近选中的10个物品，用W代替MMR 公式中的S。

通过重排规则提高多样性

重排规则

最多连续出现k篇某种笔记

小红书推荐系统的物品分为图文笔记、视频笔记。最多连续出现k=5篇图文笔记，最多连续出现k-5篇视频笔记。如果排i到i+4的全都是图文笔记，那么排在i+5的必须是视频笔记。
每k篇笔记最多出现1篇某种笔记运营推广笔记的精排分会乘以大于1的系数(boost)帮助笔记获得更多曝光。为了防止boost影响体验，限制每k-9篇笔记最多出现1篇运营推广笔记。如果排第i位的是运营推广笔记，那么排i+1到i+8的不能是运营推广笔记。
每k篇笔记最多出现1篇某种笔记运营推广笔记的精排分会乘以大于1的系数(boost)帮助笔记获得更多曝光。为了防止boost影响体验，限制每k-9篇笔记最多出现1篇运营推广笔记。如果排第i位的是运营推广笔记，那么排i+1到i+8的不能是运营推广笔记。

MMR+重排规则

每一轮先用规则排除掉R中的部分物品，得到子集R'。

MMR 公式中的R替换成子集R'，选中的物品符合规则。

DPP多样性算法

数学基础-超平形体

二维

2维空间的超平形体为平行四边形。

平行四边形中的点可以表示为 \[ x=\alpha_1v_1+ \alpha_2v_2 \] 系数$\alpha_1$和$\alpha_2$的取值范围是[0,1]

三维

2维空间的超平形体为平行六面体。

平行四边形中的点可以表示为 \[ x=\alpha_1v_1+ \alpha_2v_2+ \alpha_3v_3 \] 系数$\alpha_1$和$\alpha_2$、$\alpha_3$的取值范围是[0,1]

多维

一组向量$v_1,\cdots,v_k\in R^d$可以确定一个k维超平行体： \[ P(v_1,\cdots, v_k) = \{\alpha_1v_1+\cdots+\alpha_kv_k|0\leqslant \alpha_1,\cdots,\alpha_k \leqslant 1\} \] 要求$k\le d$,比如d=3维向量空间中有k=2维平行四边形。否则超平行体会跟拍扁了一样。

超平形体体积

构成超平形体的向量正交时，超平行体体积最大，vol=1

如果$v_1,\cdots,v_k\in R^d$线性相关，体积$vol(p)=0$

我们可以认为体积最大意味着多样性好，体积最小意味着多样性差。

对于一组向量$v_1,\cdots,v_k\in R^d$，$k\leq d$,把它们作为矩阵的列，行列式与体积满足： \[ det(V^TV) = vol(p(v_1,\cdots,v_k))^2 \]

DPP应用于多样性

精排给n个物品打分:$reward_1,\cdots, reward_n$

n 个物品的向量表征:$v_1,\cdots , v_n \in R^d$

从n个物品中选出k个物品，组成集合S

价值大:分数之和$∑_{j\in s}reward_j$越大越好
多样性好:S中k个向量组成的超平形体P(S)的体积越大越好。

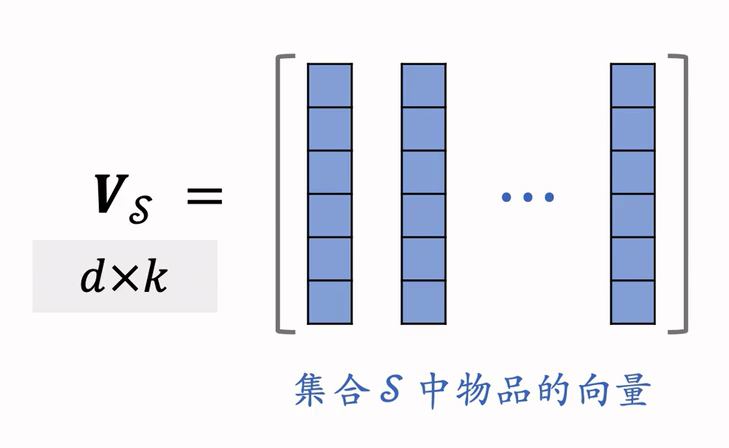
集合S中的k个物品的向量作为列，组成矩阵 $V_s\in R^{dxk}$

以这k个向量作为边，组成超平形体P(S) \[ det(V_s^TV_s) = vol(p(S))^2 \] DPP是一种传统的统计学习方法 \[ \mathop{\arg\min}\limits_{S:|S|=k} \space log det(V_s^TV_s) \] 应用于推荐系统 \[ \mathop{\arg\min}\limits_{S:|S|=k}\space \theta\cdot (\sum_{j\in S}reward_j)+(1-\theta)\cdot log det(V_s^TV_s) \] 我们构造一个nxn的矩阵$A$，它的(i,j)元素使$a_{ij}=v_i^Tv_j$，计算这个矩阵的时间复杂度是$O(n^2d)$。 \[ A_s \in R^{(k\times k)}=V_s^TV_s \] 是矩阵$A$的子矩阵，如果$i,j\in S$,则$a_{ij}$是$A_s$的一个元素。

DPP是个组合优化问题，从集合{1…,n}中选出一个大小为k的子集S。

暴力贪心算法

用S表示已选中的物品，用R表示未选中的物品，贪心算法求解 \[ \mathop{\arg\min}\limits_{i\in R}\space \theta\cdot (reward_i)+(1-\theta)\cdot log det(A_{S\cup i}) \] 对于单个i，计算 $A_{S\or i}$的行列式需要$O(|A|^3)$时间(求行列式就是需要$O(n^3)$)

对于所有的$i\in R$，计算行列式需要时间$O(|A|^3\cdot |R|)$。

需要求解上式k次才能选出k个物品。如果暴力计算行列式，那么总时间复杂度为 \[ O(|A|^3\cdot |R|\cdot k)=O(nk^4) \] 再加上计算A的时间，暴力算法总时间复杂度是： \[ O(n^2d+nk^4) \]

Hulu快速算法

给定向量$v_1,\cdots , v_n \in R^d$，需要$O(n^2d)$时间计算A

用$O(nk^2)$)时间计算所有的行列式(利用Cholesky分解)

Cholesky 分解
Cholesky 分解$A_s=LL^T$，其中L是下三角矩阵(对角线以上的元素全零)

Cholesky 分解可供计算$A_s$的行列式。
- 下三角矩阵L的行列式 det(L)等于L对角线元素乘积。
- As 的行列式为 $det(A_s)= det(L)^2=\prod_i l_{ii}^2$
已知$A_s=LL^T$，则可以快速求出所有$A_{S\cup i}$ 的 Cholesky分解(有方法可以快速算出增加一行一列的行列式)，因此可以快速算出所有 $A_{S\cup i}$ 的行列式。

DPP扩展-滑动窗口

与MMR方法一样，随着$S$增大，其中相似物品越来越多，物品向量会趋近线性相关。

DPP失效

基本概念

指标

消费指标

北极星指标

推荐系统链路

AB测试

随机分桶

分层实验

召回

协同过滤

基于物品的协同过滤 ItemCF

基本结构：

计算item相似度

运作基本流程

Swing召回通道

基本结构

基于用户的协同过滤（UserCF）

基本结构

计算User相似度

运作基本流程

协同过滤缺点

向量召回

矩阵补充 Matrix Completion

数据集

训练

缺点

运作基本流程

双塔模型

数据集

训练

Pointwise

Pairwise

Listwise

运作基本流程

模型更新

自监督学习

背景

Method

特征变换方法

自监督训练

自监督训练+正常训练

不适合召回的模型

其他方式召回

曝光过滤与链路

Bloom Filter

排序

排序模型特征

用户画像

物品画像

用户统计特征

笔记统计特征

场景特征

特征处理

粗排模型

粗排的三塔模型

精排模型

多目标模型

模型结构

估值校准：

Multi-gate Mixture-of-Experts (MMoE)

模型结构

极化现象

预估分数融合

视频播放时长建模

播放时长建模

视频完播

建模方法

融入融分公式

特征交叉

Factorized Machine

DCN

PPNet

SENet

bilinear cross

FiBiNet

用户行为序列建模

Last N

DIN模型（注意力机制）

SIM模型（长序列建模）

模型架构