常见优化函数
.
常见优化函数
梯度下降GD(决定优化方向)
梯度下降的核心思想:负梯度方向是使函数值下降最快的方向
批次梯度下降BGD

优点:在梯度下降法中,因为每次都遍历了完整的训练集,其能保证结果为全局最优
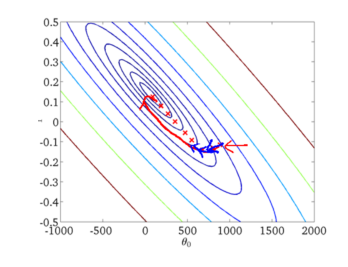
缺点:我们需要对于每个参数求偏导,且在对每个参数求偏导的过程中还需要对训练集遍历一次,当训练集(m)很大时,计算费时
解决方法:使用minibatch去更新
随机梯度下降
为了解决BGD耗时过长,它是利用单个样本的损失函数对θ求偏导得到对应的梯度,来更新θ,更新过程如下:

速度快,但受抽样影响大,噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
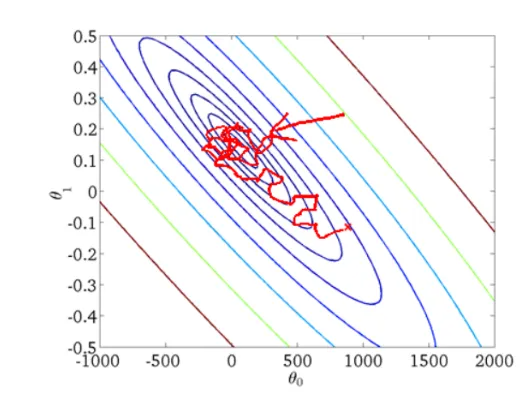
因为每一次迭代的梯度受抽样的影响比较大,学习率需要逐渐减少,否则模型很难收敛。在实际操作中,一般采用线性衰减: \[ \eta_k=(1-\alpha)\eta_0+\alpha\eta_{\tau} \]
\[ \alpha=\frac{k}{\tau} \]
\(\eta_0\):初始学习率
\(\eta_{\tau}\): 最后一次迭代的学习率
\(\tau\):自然迭代次数
\(\eta_{\tau}\)设为\(\eta_0\)的1%,k一般设为100的倍数。
优点:收敛速度快
缺点:
训练不稳定:噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
选择适当的学习率可能很困难。 太小的学习率会导致收敛性缓慢,而学习速度太大可能会妨碍收敛,并导致损失函数在最小点波动。
无法逃脱鞍点
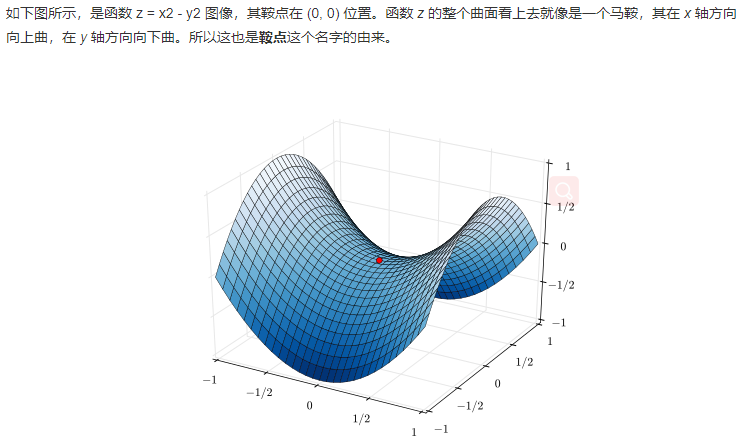
min-batch 小批量梯度下降MBGD
算法的训练过程比较快,而且也要保证最终参数训练的准确率
m表示一个批次的数据个数
动量方法
Momentum随机梯度下降
核心思想:Momentum借用了物理中的动量概念,即前一次的梯度也会参与运算。为了表示动量,引入了一阶动量m。是之前的梯度的累加,但是每回合都有一定的衰减。公式如下:
\[
m_t=\beta m_{t-1}+(1-\beta)\cdot g_t
\]
\[ w_{t+1}=w_t-\eta \cdot m_t \]
\(g_t\): 为第t次计算的梯度(就是现在要算这次)
\(m_{t-1}\): 为之前梯度的累加
\(\beta\): 动量因子
所以当前权值的改变受上一次改变的影响,类似加上了惯性。
优点:momentum能够加速SGD收敛,抑制震荡。并且动量有机会逃脱局部极小值(鞍点)。
- 在梯度方向改变时,momentum能够降低参数更新速度,从而减少震荡;
- 在梯度方向相同时,momentum可以加速参数更新, 从而加速收敛。
Nesterov动量随机梯度下降法
Nesterov是Momentum的变种。与Momentum唯一区别就是,计算梯度的不同。Nesterov动量中,先用当前的速度临时更新一遍参数,在用更新的临时参数计算梯度。
在momentum更新梯度时加入对当前梯度的校正,让梯度“多走一步”,可能跳出局部最优解: \[ w_t^*=\beta m_{t-1}+w_t \]
\[ m_t=\beta m_{t-1}+(1-\beta)\cdot g_t \]
\[ w_{t+1}=w_t-\eta \cdot m_t \]
这里的\(g_t\)用临时点\(w_t^*\)计算的
更新学习率方法
Adagrad
引入二阶动量,根据训练轮数的不同,对学习率进行了动态调整:

缺点:仍然需要人为指定一个合适的全局学习率,同时网络训练到一定轮次后,分母上梯度累加过大使得学习率为0而导致训练提前结束。
Adadelta(不是很懂)

RMSProp
AdaGrad算法在迭代后期由于学习率过小,可能较难找到一个有用的解。为了解决这一问题,RMSprop算法对Adagrad算法做了一点小小的修改,RMSprop使用指数衰减只保留过去给定窗口大小的梯度,使其能够在找到凸碗状结构后快速收敛。RMSProp法可以视为Adadelta法的一个特例,即依然使用全局学习率替换掉Adadelta法中的\(s_t\):
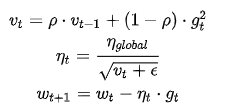
推荐\(\eta_{global}=1,\rho=0.9,\epsilon=10^{-6}\)
缺点:依然使用了全局学习率,需要根据实际情况来设定 优点:
- 分母不再是一味的增加,它会重点考虑距离它较近的梯度(指数衰减的效果)
- 只用了部分梯度加和而不是所有,这样避免了梯度累加过大使得学习率为0而导致训练提前结束。
Adam
https://zhuanlan.zhihu.com/p/377968342
Adam公式如下: \[ m_t:=beta_1*m_{t-1}+(1-beta_1)*g \]
\[ v_t:=beta_2*v_{t-1}+(1-beta_2)*g*g \]
\[ variable:=variable-lr_t*\frac{m_t}{\sqrt{v_t+\epsilon}} \]
\(m_t\)可以理解为求历史梯度加强平均,思想来自动量方法,防止震荡。
\(v_t\)则是用于调整lr的,即是\(\frac{lr}{\sqrt{v_t+\epsilon}}\),
在迭代过程中,如果某一维度一直以很小的梯度进行更新,证明此方向梯度变换较为稳定,因此可以加大学习率,以较大的学习率在此维度更新,体现在公式上就是:对历史梯度平方进行一阶指数平滑后,公式2会得到一个很小的值,公式3中的自适应学习率会相对较大
相反,某一维度在迭代过程中一直以很大的梯度进行更新,明此方向梯度变换较为剧烈(不稳定),因此可减小学习率,以较小的学习率在此维度更新 体现在公式上就是:对历史梯度平方进行一阶指数平滑后,公式2则会得到一个很大的值,公式3中的自适应学习率会相对较小
\(v_t\)也可以解决梯度稀疏的问题;频繁更新的梯度将会被赋予一个较小的学习率,而稀疏的梯度则会被赋予一个较大的学习率,通过上述机制,在数据分布稀疏的场景,能更好利用稀疏梯度的信息,比标准的SGD算法更有效地收敛。
常见优化函数问题
SGD和Adam谁收敛的比较快?谁能达到全局最优解?
SGD算法没有动量的概念,SGD和Adam相比,缺点是下降速度慢,对学习率要求严格。
而Adam引入了一阶动量和二阶动量,下降速度比SGD快,Adam可以自适应学习率,所以初始学习率可以很大。
SGD相比Adam,更容易达到全局最优解。主要是后期Adam的学习率太低,影响了有效的收敛。
我们可以前期使用Adam,后期使用SGD进一步调优。
adam用到二阶矩的原理是什么
引入二阶动量,根据训练轮数不同对学习率进行调整。
可以看出来,公式将前面的训练梯度平方加和,在网络训练的前期,由于分母中梯度的累加(\(v_t\))较小,所以一开始的学习率\(\eta_t\)比较大;随着训练后期梯度累加较大时,\(\eta_t\)逐渐减小,而且是自适应地减小。
而且如果某个维度频繁震荡梯度大,学习率就降低;如果梯度小而稳定,学习率就大。
Batch的大小如何选择,过大的batch和过小的batch分别有什么影响
Batch选择时尽量采用2的幂次,如8、16、32等
在合理范围内,增大Batch_size的好处:
- 提高了内存利用率以及大矩阵乘法的并行化效率。
- 减少了跑完一次epoch(全数据集)所需要的迭代次数,加快了对于相同数据量的处理速度。
盲目增大Batch_size的坏处:
- 提高了内存利用率,但是内存容量可能不足。
- 跑完一次epoch(全数据集)所需的迭代次数减少,要想达到相同的精度,其所花费的时间大大增加,从而对参数的修正也就显得更加缓慢。
- Batch_size增大到一定程度,其确定的下降方向已经基本不再变化。
Batch_size过小的影响:
- 训练时不稳定,可能不收敛
- 精度可能更高。