RippleNet
.
Background
CF: sparsity, cold start
KG-benefit:
- KG introduces semantic relatedness among items, which can help find their latent connections and improve the precision of recommended items;
- KG consists of relations with various types, which is helpful for extending a user’s interests reasonably and increasing the diversity of recommended items;
- KG connects a user’s historical records and the recommended ones, thereby bringing explainability to recommender systems.
Existing KG model:
- embedding-based method: DKN, CKE, SHINE, but more suitable for in-graph applications
- path-based method: rely heavily on manually designed meta-paths
so the author proposes RippleNet:
- combine embedding-based and path-based() methods
- RippleNet incorporates the KGE methods into recommendation naturally
by preference propagation;
- RippleNet can automatically discover possible paths from an item in a user’s history to a candidate item.
- RippleNet incorporates the KGE methods into recommendation naturally
by preference propagation;
Method
专注于挖掘KG中用户感兴趣的实体!!
Input
interaction matrix Y and knowledge graph G
Some definition
Relevant entity
the set of k-hop relevant entities for user u is defined as

\(\varepsilon_u^0=V_u = \{v|y_{uv}=1\}\) is the items which the user interacts with, and they can link with entities in knowledge graph
can be seen as the seed set of user u in KG(就是user如何参与到KG中)
Ripple set

Model
First layer propagation

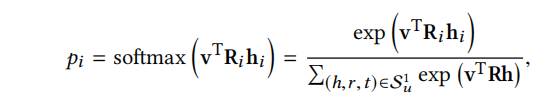
v: embedding of item. Item embedding can incorporate one-hot ID , attributes of an item, based on the application scenario.
r: embedding of relation between head entity and tail entity.
h: embedding of head entity.
t: embedding of tail entity.
attention weight \(p_i\) can be regarded as the similarity of item v and the entity \(h_i\) measured in the space of relation \(r_i\).
\(r_i\) is important, since an item-entity pair may have different similarities when measured by different relations
Multi-layer
the second layer just replace v with \(o_u^1\)
\[ p_i = softmax(o_u^{1T}R_ih_i) = \frac{exp(o_u^{1T}T_ih_i)}{\sum_{(h,r,t)\in S_u^2}exp(o_u^{1T}Rh)} \]
\[ o_u^2 = \sum_{(h_i,r_i,t_i)\in S_u^2}p_it_i \]
and third layer replace \(o_u^1\) with \(o_u^2\)
while
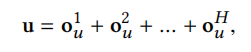
predict
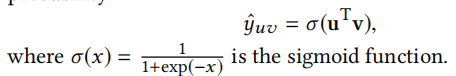
Whole process
Propagation only used in KG-graph

模型不断扩散,不断获取更高层数neighbor的信息,最后通过加在一起汇总
所以与曾经互动过的item有关系的实体信息(KG信息)汇总为user embedding,最后再与没互动过的item计算估计互动概率,
所以是否能理解为user汇总的KG信息
Loss Function(还没想明白)
别人的笔记::
这里的分成三个部分:分别是预测分数的交叉熵损失,知识图谱特征表示的损失,参数正则化的损失:
预测部分的损失很好理解,就是用户和该item之间的预测值和真实值的loss
知识图谱特征表示的损失:我们在计算每个阶段的加权求和时上面说了,假设前提是hR=t,这是假设,所以我们需要设一个loss让模型学习,学习的内容就是hR和t之间计算相似度后,预测0,1是否相似
l2正则化损失:每一个hop中h,r,t分别和自己相乘后,求和再求均值得到一个值,即为该loss(这里我理解的不是很深,有了解的可以评论区说说)
Experiment
Other
ripple set 可能太大,
在RippleNet中,我们可以对固定大小的邻居集进行采样,而不是使用完整的纹波集来进一步减少计算开销。