常见损失函数
常见损失函数及常见问题
常见损失函数
损失函数用来评价模型的预测值和真实值不一样的程度,在模型正常拟合的情况下,损失函数值越低,模型的性能越好。不同的模型用的损失函数一般也不一样。
损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差值,结构风险损失函数是指经验风险损失函数加上正则项。
常用
用于回归:
绝对值损失函数
\[ L(Y,f(x)) = |Y-f(x)| \]
平方损失函数
\[ L(Y,f(x)) = (Y-f(x))^2 \]
对n个数据求平方损失后加和求平均叫均方误差MSE,常在线性回归使用 \[ \frac{1}{N}\sum_n(Y-f(x))^2 \]
用于分类
0-1损失函数(zero-one loss)
\[ L(Y,f(x)) = \left\{ \begin{array}{rcl} 1 & &{Y!=f(x)}\\ 0 & &{Y=f(x)} \end{array} \right. \]
非黑即白,过于严格,用的很少,比如感知机用。
可通过设置阈值放宽条件 \[ L(Y,f(x)) = \left\{ \begin{array}{rcl} 1 & &{|Y-f(x)>=T}\\ 0 & &{|Y-f(x)<T} \end{array} \right. \]
对数损失函数(log loss)
\[ L(Y,P(Y|X)) = -logP(Y|X) \]
Y为真实分类,\(P(Y|X)\)为X条件下分类为Y的概率。用于最大似然估计,等价于交叉熵损失函数
加负号原因:习惯在模型更准确的情况下,loss函数越小
加log原因:这和最大(极大)似然估计有关,对数损失是用于最大似然估计的。
最大似然估计:利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值。
我们假定一组参数(\(\Theta\))在一堆数据(样本结果\(x_1,x_2...\))下的似然值为P(θ|x1,x2,...,xn)=P(x1|θ)*P(x2|θ)*...*P(xn|θ),可以看出来,似然值等于每一条数据在这组参数下的条件概率之积。求概率是乘性,而求损失是加性,所以才需要借助log(对数)来转积为和,另一方面也是为了简化运算。
对数损失在逻辑回归和多分类任务上广泛使用。交叉熵损失函数的标准型就是对数损失函数,本质没有区别。
交叉熵损失函数
双分类: \[ L(Y,f(x)) = -[Ylnf(x)+(1-y)ln(1-f(x))] \] 多分类: \[ L(Y,f(x)) = -Ylnf(x) \]
合页损失函数(hinge loss)
\[ L(Y,f(x)) = max(0, 1-Y\cdot f(x)) \]
SVM就是使用的合页损失,还加上了正则项。公式意义是,当样本被正确分类且函数间隔大于1时,合页损失是0,否则损失是\(1-Y\cdot f(x)\).
SVM中\(Y\cdot f(x)\)为函数间隔,对于函数间隔:
正负
当样本被正确分类时,\(Y\cdot f(x)>0\);当样本被错误分类时,\(Y\cdot f(x)<0\)。
大小
\(Y\cdot f(x)\)的绝对值代表样本距离决策边界的远近程度。\(Y\cdot f(x)\)的绝对值越大,表示样本距离决策边界越远。因此,我们可以知道:
当\(Y\cdot f(x)>0\)时,\(Y\cdot f(x)\)的绝对值越大表示决策边界对样本的区分度越好
当\(Y\cdot f(x)<0\)时,\(Y\cdot f(x)\)的绝对值越大表示决策边界对样本的区分度越差
指数损失函数(exponential loss)
\[ L(Y,f(x)) = exp(-Y\cdot f(x)) = \frac{exp(f(x))}{exp(Y)} \]
常用于AdaBoost算法,
那么为什么AdaBoost算法使用指数损失函数,而不使用其他损失函数呢?
这是因为,当前向分步算法的损失函数是指数损失函数时,其学习的具体操作等价于AdaBoost算法的学习过程。
用于分割

用于检测

常见损失函数问题
交叉熵相关
交叉熵函数与最大似然函数的联系和区别?
区别:
交叉熵函数使用来描述模型预测值和真实值的差距大小,越大代表越不相近;
极大似然就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值!即“模型已定,参数未知”
联系:
交叉熵函数可以由最大似然函数在伯努利分布的条件下推导出来,或者说最小化交叉熵函数的本质就是对数似然函数的最大化。
在用sigmoid作为激活函数的时候,为什么要用交叉熵损失函数,而不用均方误差损失函数?
另一个问法其实是在分类问题中为什么不用均方误差做损失函数。
sigmoid作为激活函数的时候,如果采用均方误差损失函数,那么这是一个非凸优化问题,不宜求解。而采用交叉熵损失函数依然是一个凸优化问题,更容易优化求解。(凸优化问题中局部最优解同时也是全局最优解)。而且\(\frac{dL}{dW}\)中,有地方为0,如果参数刚好导致\(\frac{dL}{dW}\)为0,参数就不会更新。

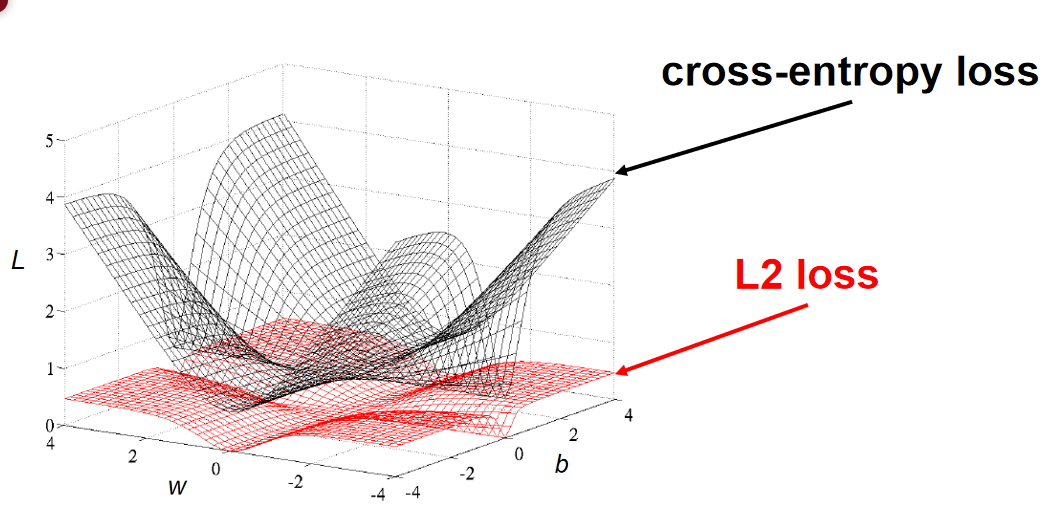
- 因为交叉熵损失函数可以完美解决平方损失函数权重更新过慢的问题,具有“误差大的时候,权重更新快;误差小的时候,权重更新慢”的良好性质。
方损失函数权重更新过慢原因:
梯度更新公式为:

这里a是预测值,y是实际值
有\(\sigma'(z)\)这一项而sigmoid函数两端梯度很小,导致参数更新缓慢。
而交叉熵函数不会有这个问题虽然有\(\sigma(z)\)但没有\(\sigma'(z)\),求导detail如下:

交叉熵和均分函数区别

如何推导出交叉熵函数

为什么交叉熵函数有log项
第一种:因为是公式推导出来的,比如第六题的推导,推导出来的有log项。
第二种:通过最大似然估计的方式求得交叉熵公式,这个时候引入log项。这是因为似然函数(概率)是乘性的,而loss函数是加性的,所以需要引入log项“转积为和”。而且也是为了简化运算。
交叉熵的设计思想
交叉熵函数的本质是对数函数。
交叉熵函数使用来描述模型预测值和真实值的差距大小,越大代表越不相近。
交叉熵损失函数可以完美解决平方损失函数权重更新过慢的问题,具有“误差大的时候,权重更新快;误差小的时候,权重更新慢”的良好性质。
对数损失在逻辑回归和多分类任务上广泛使用。交叉熵损失函数的标准型就是对数损失函数,本质没有区别。
CV相关
Yolo损失函数
Yolo是用于模板检测的模型
Yolo的损失函数由四部分组成:

- 对预测的中心坐标做损失

- 对预测边界框的宽高做损失

- 对预测的类别做损失

- 对预测的置信度做损失

我们发现每一项loss的计算都是L2 loss(平方差),即使是分类问题也是。所以说yolo是把分类问题转为了回归问题。
IOU与MIOU计算
IOU(Intersection over Union),交集占并集的大小。
mIOU一般都是基于类进行计算的,将每一类的IOU计算之后累加,再进行平均,得到的就是mIOU。
其它
KL散度
相对熵(relative entropy),又被称为Kullback-Leibler散度(Kullback-Leibler divergence)或信息散度(information divergence),是两个概率分布(probability distribution)间差异的非对称性度量 。在信息理论中,相对熵等价于两个概率分布的信息熵(Shannon entropy)的差值。
设,
是随机变量
上的两个概率分布,则在离散和连续随机变量的情形下,相对熵的定义分别为:
为理论概率分布,
为模型预测概率分布,而KL就是度量这两个分布的差异性,当然差异越小越好,所以KL也可以用作损失函数。