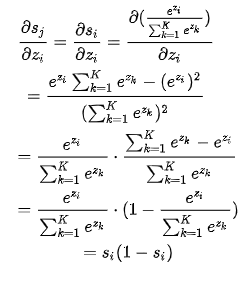常见激活函数
.
常见激活函数
激活函数作用:加入非线性因素
Sigmoid
\[ \sigma(x) = \frac{1}{1+exp(-x)} \]
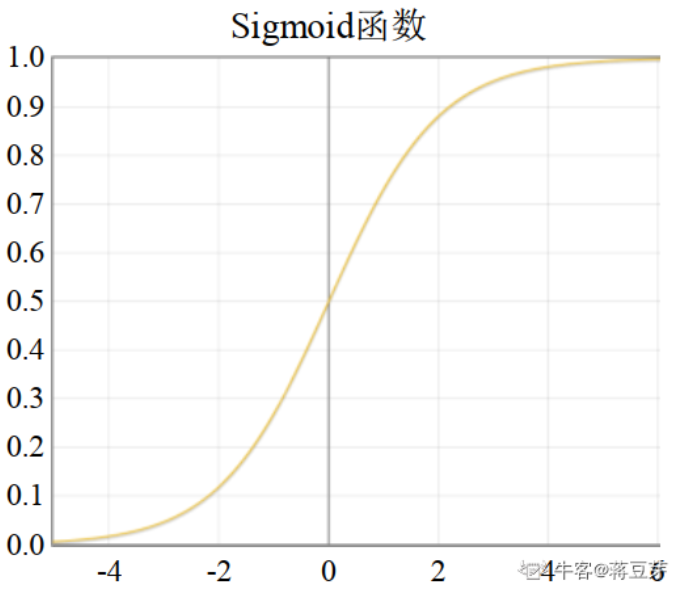
输出的值范围在[0,1]之间。但是sigmoid型函数的输出存在均值不为0的情况,并且存在梯度消失的问题,在深层网络中被其他激活函数替代。在逻辑回归中使用的该激活函数用于输出分类。
求导公式
链式法则
梯度消失原因:
\[ \sigma'(x) = \sigma\space \cdot (1-\sigma) \]
- sigmoid函数两边的斜率趋向0,很难继续学习
- sigmoid导数两个部分都小于1,在深层神经网络中,靠前layer参数会因为后面多层sigmoid导数叠加(链式法则)导致更新的特别慢。
缺点解决办法
- 在深层网络中被其他激活函数替代。如
ReLU(x)、Leaky ReLU(x)等 - 在分类问题中,sigmoid做激活函数时,使用交叉熵损失函数替代均方误差损失函数。
- 采用正确的权重初始化方法(让初始化的数据尽量不要落在梯度消失区域)
- 加入BN层(同上,避免数据落入梯度消失区)
- 分层训练权重
tanh
\[ tanh(x) = \frac{e^x-e^{(-x)}}{e^x+e^{(-x)}} =\frac{e^{2x}-1}{e^{2x}+1}= 2 \cdot sigmoid(2x)-1 \]
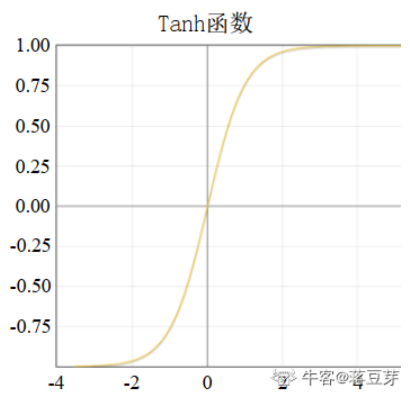
tanh(x)型函数可以解决sigmoid型函数的期望(均值)不为0的情况。函数输出范围为(-1,+1)。但tanh(x)型函数依然存在梯度消失的问题。
在LSTM中使用了tanh(x)型函数。
Relu
ReLU(x)型函数可以有效避免梯度消失的问题,公式如下:
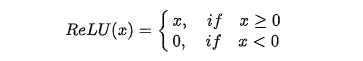
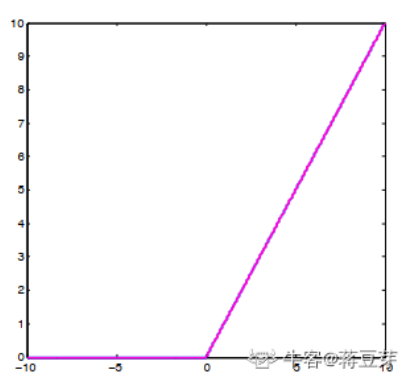
ReLU(x)型函数的缺点是负值成为“死区”,神经网络无法再对其进行响应。Alex-Net使用了ReLU(x)型函数。当我们训练深层神经网络时,最好使用ReLU(x)型函数而不是sigmoid(x)型函数。
ReLU梯度稳定,值还比sigmoid大,所以可以加快网络训练。
但是要注意,我们在输入图像时就要注意,应该使用Min-Max归一化,而不能使用Z-score归一化。(避免进入死区)
在0点不可导
人为将梯度规定为0(源码就是这么写的)
Relu6
Relu的正值输出是[0,无穷大],但计算机内存优先,所以限定relu最大值为6
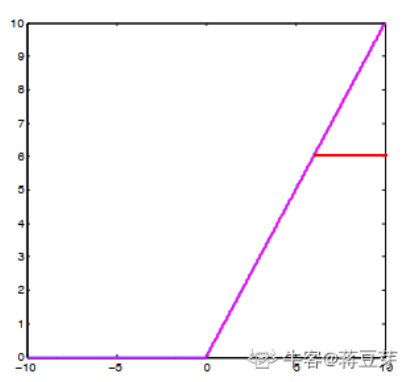
LeakyRelu
为负值增加了一个斜率,缓解了“死区”现象,公式如下:
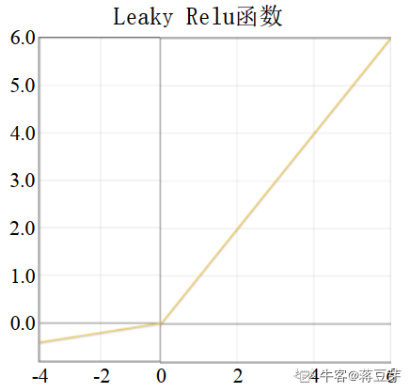
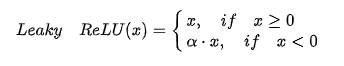
Leaky ReLU(x)型函数缺点是,超参数a(阿尔法)合适的值不好设定。当我们想让神经网络能够学到负值信息,那么使用该激活函数。
P-Relu 参数化Relu
数化ReLU(P-ReLU)。参数化ReLU为了解决超参数a(阿尔法)合适的值不好设定的问题,干脆将这个参数也融入模型的整体训练过程中。也使用误差反向传播和随机梯度下降的方法更新参数。
R-Relu 随机化Relu
就是超参数a(阿尔法)随机化,让不同的层自己学习不同的超参数,但随机化的超参数的分布符合均值分布或高斯分布。
Mish激活函数
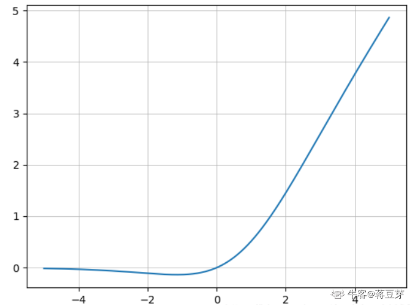 \[
Mish(x) = x\cdot tanh(log(1+e^x))
\]
\[
Mish(x) = x\cdot tanh(log(1+e^x))
\]
在负值中,允许有一定的梯度流入。
ELU指数化线性单元
也是为了解决死区问题,公式如下:
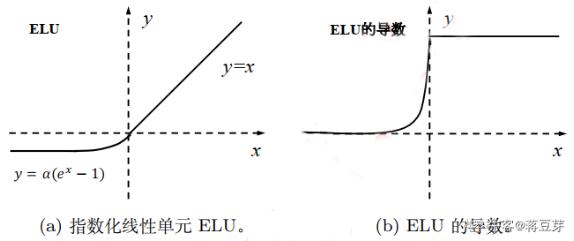

缺点是指数计算量大。
Maxout
就是用一个MLP层作为激活函数。

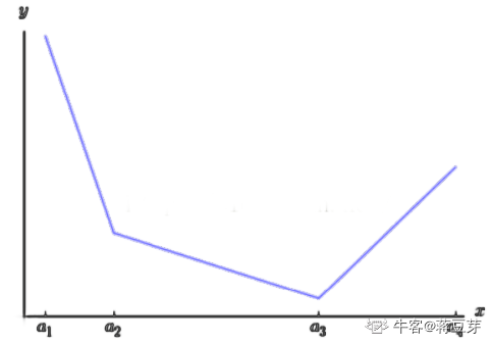
与常规的激活函数不同,Maxout是一个可以学习的分段线性函数。其原理是,任何ReLU及其变体等激活函数都可以看成分段的线性函数,而Maxout加入的一层神经元正是一个可以学习参数的分段线性函数。
优点是其拟合能力很强,理论上可以拟合任意的凸函数。缺点是参数量激增!在Network-in-Network中使用的该激活函数。
Softmax求导
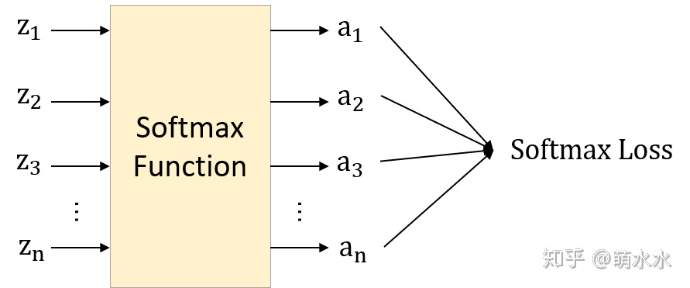
要结合交叉熵loss函数考虑
\(\frac{dL}{dz}=\frac{dL}{da}\cdot \frac{da}{dz}\)
假设第j个类别是正确的,\(y_j=1\),其它为0
\(L = -\sum_{i=1}^ny_iln(a_i)\)
\(\frac{dL}{da} = -y_iln(a_j)=-ln(a_j)\)

所以最终Loss只跟label类别有关
所以当i=j:
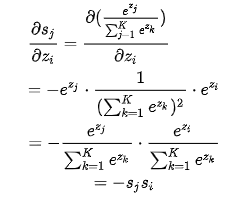
当i!=j: