LightGCN

Posted on 2023-02-24 Edited on 2024-06-19 In RecSys

Background

question: why concentrated to sum

Main contributes

We empirically show that two common designs in GCN, feature transformation and nonlinear activation, have no positive effect on the effectiveness of collaborative filtering.

GCN is originally proposed for node classification on the attributed graph, where each node has rich attributes as input features; whereas in the user-item interaction graph for CF, each node (user or item) is only described by a one-hot ID, which has no concrete semantics besides being an identifier.
Propose LightGCN.

Analyze about NGCF

Brief

完全想不起来的话建议先看NGCF的笔记

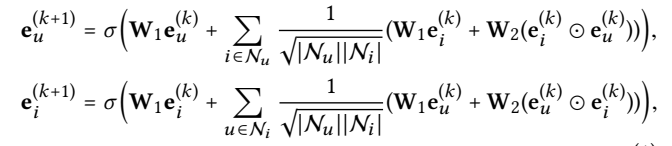
## Some experiment

Method

Using ablation studies, implement three simplified variants of NGCF:

NGCF-f: which removes the feature transformation matrices $W1$ and $W2$.
NGCF-n: which removes the non-linear activation function $ σ$.
NGCF-fn: which removes both the feature transformation matrices and non-linear activation function.

Note: Since the core of GCN is to refine embeddings by propagation, we are more interested in the embedding quality under the same embedding size. Thus, we change the way of obtaining final embedding from concatenation (i.e., $e_u^*=e_u^{(0)}\|e_u^{(1)}\|...\|e_u^{(L)}$) to sum(i.e., $e_u^*=e_u^{(0)}+e_u^{(1)}+...+e_u^{(L)}$).

This change has little effect on NGCF’s performance but makes the following ablation studies more indicative of the embedding quality refined by GCN.

Result

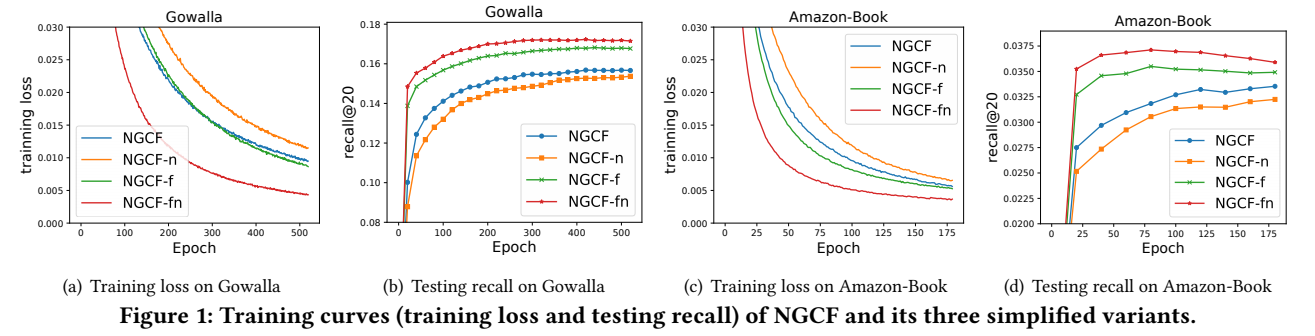
Adding feature transformation imposes negative effect on NGCF, since removing it in both models of NGCF and NGCF-n improves the performance significantly;
Adding nonlinear activation affects slightly when feature transformation is included, but it imposes negative effect when feature transformation is disabled.
As a whole, feature transformation and nonlinear activation impose rather negative effect on NGCF, since by removing them simultaneously, NGCF-fn demonstrates large improvements over NGCF.

Conclusion

The deterioration of NGCF stems from the training difficulty(underfitting), rather than overfitting, because:

Such lower training loss of NGCF-fn successfully transfers to better recommendation accuracy.
NGCF is more powerful and complex, but it demonstrates higher training loss and worse generalization performance than NGCF-f.

Model of LightGCN

Consisting four parts:

initialize users and items embedding.
Light Graph Convolution (LGC)
Layer Combination
Model Prediction

Light Graph Convolution (LGC)

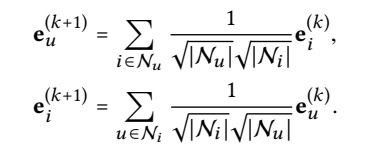
$ $： symmetric normalization, which can avoid the scale of embeddings increasing with graph convolution operations. Here can use other normalization, but symmetric normalization has good performance.

Note: Without self-connection, because the layer combination operation of LightGCN captures the same effect as self-connections.

Layer Combination

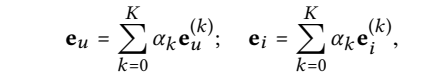
$α_k$can be treated as a hyperparameter to be tuned manually, or as a model parameter, and setting $α_k$ uniformly as $1/(K + 1)$ leads to good performance in general.

This is probably because the training data does not contain sufficient signal to learn good α that can generalize to unknown data.

The reason of using the Layer Combination:

With the increasing of the number of layers, the embeddings will be over-smoothed [27]. Thus simply using the last layer is problematic.
The embeddings at different layers capture different semantics.
Combining embeddings at different layers with weighted sum captures the effect of graph convolution with self-connections, an important trick in GCNs.

Model Prediction

inner product

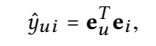
Matrix form

Similar to NGCF, and there are some explanations in detail in NGCF note.

Light Graph Convolution:

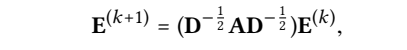
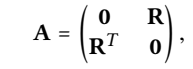
Layer combination:

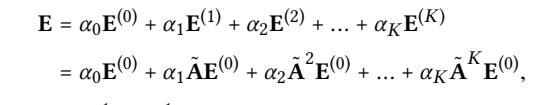
Analyze about LightGCN

Relation with SGCN

Purpose: by doing layer combination, LightGCN subsumes the effect of self-connection thus there is no need for LightGCN to add self-connection in adjacency matrix.

SGCN: a recent linear GCN model that integrates self-connection into graph convolution.

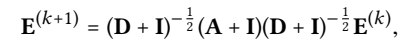
In the following analysis, we omit the $(D + I)^{-\frac{1}{2}}$ terms for simplicity, since they only re-scale embeddings.

The above derivation shows that, inserting self-connection into A and propagating embeddings on it, is essentially equivalent to a weighted sum of the embeddings propagated at each LGC layer.

because $AE^{(0)}=E^{(1)}$...$A^KE^{(0)}=E^{(K)}$

Relation with APPNP

Purpose: shows the underlying equivalence between LightGCN and APPNP, thus our LightGCN enjoys the sames benefits in propagating long-range with controllable overs-moothing.

APPNP: a recent GCN variant that addresses over-smoothing. APPNP complements each propagation layer with the starting features.

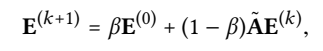
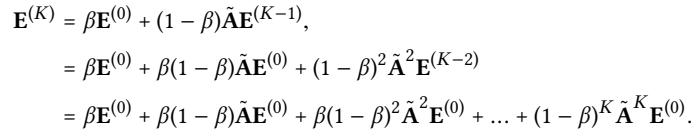
also equivalent to a weighted sum of the embeddings propagated at each LGC layer.

Second-Order Embedding Smoothness

Purpose: providing more insights into the working mechanism of LightGCN.

below is influence from2-order neighbor to target node.

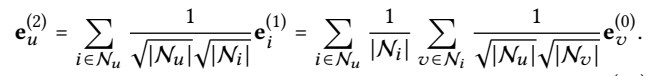
conclusion: the influence of a second-order neighbor v on u is determined by

the number of co-interacted items, the more the larger.
the popularity of the co-interacted items, the less popularity (i.e., more indicative of user personalized preference) the larger
the activity of v, the less active the larger.

Model Train

Loss function

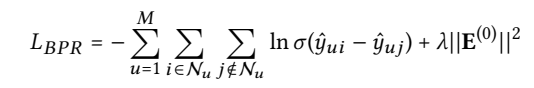
Optimizer: Adam

No dropout strategy

The reason is that we do not have feature transformation weight matrices in LightGCN, thus enforcing L2 regularization on the embedding layer is sufficient to prevent overfitting.

Experiment

compared with NGCF

LightGCN performs better than NGCF and NGCF-fn, as NGCF-fn still contains more useless operations than LightGCN.
Increasing the number of layers can improve performance, but the benefits diminish. Increasing the layer number from 0 to 1 leads to the largest performance gain, and using a layer number of 3 leads to satisfactory performance in most cases.
LightGCN consistently obtains lower training loss, which indicates that LightGCN fits the training data better than NGCF. Moreover, the lower training loss successfully transfers to better testing accuracy, indicating the strong generalization power of LightGCN. In contrast, the higher training loss and lower testing accuracy of NGCF reflect the practical difficulty to train such a heavy model it well.

Ablation and Effectiveness Analyses

Impact of Layer Combination

Using models:

LightGCN
LightGCN-single: does not use layer combination

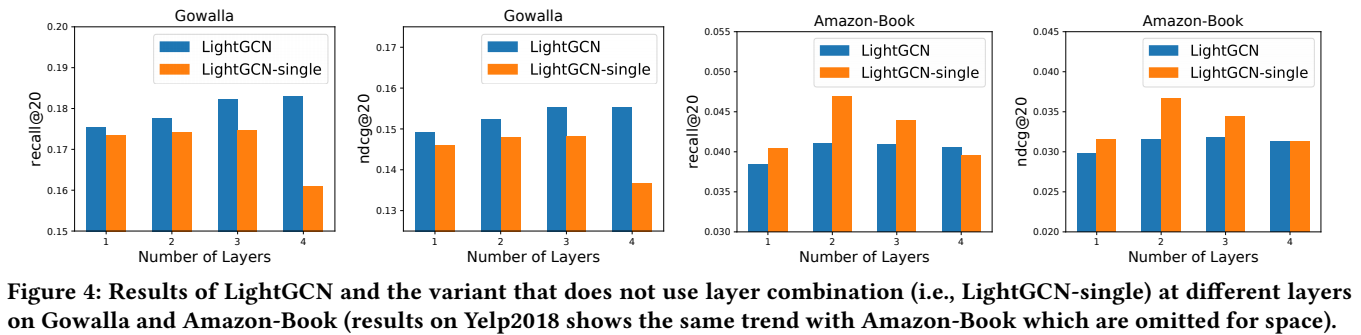
Conclusion

Focusing on LightGCN-single, we find that its performance first improves and then drops when the layer number increases from 1 to 4. This indicates that smoothing a node’s embedding with its first-order and secondorder neighbors is very useful for CF, but will suffer from oversmoothing issues when higher-order neighbors are used.
Focusing on LightGCN, we find that its performance gradually improves with the increasing of layers even using 4 layers. This justifies the effectiveness of layer combination for addressing over-smoothing.
we find that LightGCN consistently outperforms LightGCN-single on Gowalla, but not on AmazonBook and Yelp2018. There are two reason:
1. LightGCN-single is special case of LightGCN that sets αK to 1 and other αk to 0;
2. we do not tune the $αk$ and simply set it as $\frac{1}{K+1}$ uniformly for LightGCN.

Impact of Symmetric Sqrt Normalization

Setting:

LightGCN-L: normalization only at the left side (i.e., the target node’s coefficient).
LightGCN-R: the right side (i.e., the neighbor node’s coefficient).
LightGCN-L1: use L1 normalization( i.e., removing the square root).
LightGCN-L1-L: use L1 normalization only on the left side.
LightGCN-L1-R: use L1 normalization only on the right side.

Conclusion

The best setting in general is using sqrt normalization at both sides (i.e., the current design of LightGCN). Removing either side will drop the performance largely.
The second best setting is using L1 normalization at the left side only (i.e., LightGCN-L1-L). This is equivalent to normalize the adjacency matrix as a stochastic matrix by the in-degree(norm后矩阵无对称性).
Normalizing symmetrically on two sides is helpful for the sqrt normalization, but will degrade the performance of L1 normalization.

Analysis of Embedding Smoothness

Object: Making sure such smoothing（有点像聚类的感觉） of embeddings is the key reason of LightGCN’s effectiveness.

Method: we first define the smoothness of user embeddings as(用于衡量2-order neighbor的embedding差别大小，是否合理聚类的感觉):

where the L2 norm on embeddings is used to eliminate the impact of the embedding’s scale.

result:

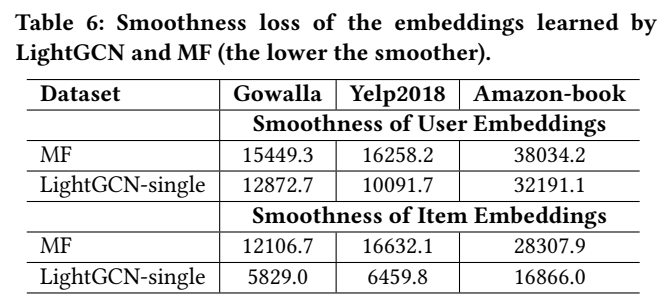
Conclusion: the smoothness loss of LightGCN-single is much lower than that of MF.

This indicates that by conducting light graph convolution, the embeddings become smoother and more suitable for recommendation.

Hyper-parameter Studies

object: Ensure the L2 regularization coefficient $λ$

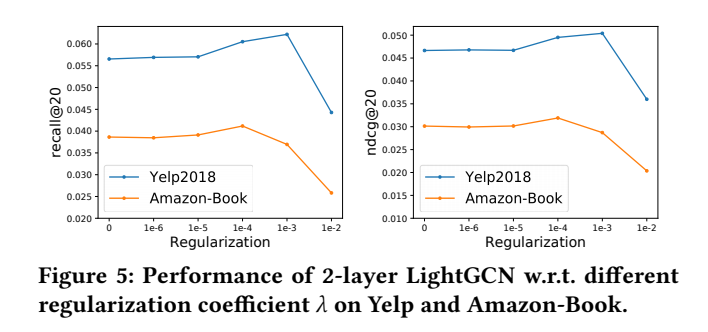
Conclusion:

LightGCN is relatively insensitive to λ.
Even when λ sets to 0, LightGCN is better than NGCF, which additionally uses dropout to prevent overfitting. This shows that LightGCN is less prone to overfitting
When λ is larger than 1e−3, the performance drops quickly, which indicates that too strong regularization will negatively affect model normal training and is not encouraged.