KGAT

Posted on Edited on In ,

.

Background

利用KG作为辅助信息，并将KG与user-item graph 整合为一个图

Background

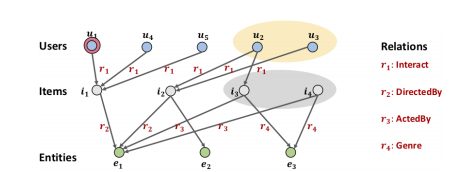
image-20230224155340260

Previous model:

CF: behaviorally similar users would exhibit similar preference on items.

focus on the histories of similar users who also watched \(i1\), i.e., \(u4\) and \(u5\);

SL: transform side information into a generic feature vector, together with user ID and item ID, and feed them into a supervised learning (SL) model to predict the score.

emphasize the similar items with the attribute \(e1\), i.e.$ i2$.

current problem:

existing SL methods fail to unify them, and ignore other relationships in the graph:

  1. the users in the yellow circle who watched other movies directed by the same person \(e_1\).
  2. the items in the grey circle that share other common relations with \(e_1\).

User-Item Bipartite Graph: \(G_1\)

\[ \{(u,y_{ui},i)|u\in U, i\in I\} \] \(U\): user sets

\(I\): item sets

\(y_{ui}\): if user \(u\) interacts with item \(i\) \(y_{ui}\)=, else \(y_{ui}\)=0.

Knowledge Graph \(G2\)

\[ \{(h,r,t)|h,t\in E, r\in R\} \]

\(t\) there is a relationship \(r\) from head entity h to tail entity \(t\).

\(CKG\): Combination of \(G1\) and \(G2\)

  1. represent each user-item behavior as a triplet $ (u, Interact,i)\(, where\) y^{ui}$ = 1.
  2. we establish a set of item-entity alignments

\[ A = \{(i, e)|i ∈ I, e ∈ E \} \]

  1. based on the item-entity alignment set, the user-item graph can be integrated with KG as a unified graph.

\[ G = \{(h,r,t)|h,t ∈ E^′,r ∈R^′\} \]

\[ E^′ = E ∪ U \]

\[ R^′ = R ∪ {Interact} \]

Methodology

image-20230222185609261

KGAT has three main components:

  1. Embedding layer
  2. Attentive embedding propagation layer
  3. prediction layer

Embedding layer

Using TransR to calculate embedding

Assumption: if a triplet (h,r,t) exist in the graph, \[ e^r_h+e_r\approx e_t^r \] Herein, \(e^h\), \(e^t\) ∈ \(R^d\) and \(e^r\) ∈ \(R^k\)are the embedding for h, t, and r; and \(e^r_h\), \(e^r_t\) are the projected representations of \(e^h\), \(e^t\) in the relation r’s space.

Plausibility score:

image-20230222193700417

\(W_r ∈ R^{k\times d}\) is the transformation matrix of relation r, which projects entities from the d-dimension entity space into the k dimension relation space.

A lower score suggests that the triplet is more likely to be true.

Loss:

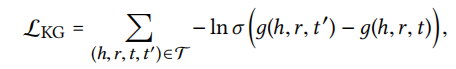
image-20230222195306105

\(\{(h,r,t,t^′ )|(h,r,t) \in G, (h,r,t^′ ) \notin G\}\), \((h,r,t^′ )\) is a negative sample constructed by replacing one entity in a valid triplet randomly.

σ(·): sigmoid function, ——》将分数映射再0-1区间，归一化

？？？？？？？？？？？why this layer model working as a regularizer

Attentive Embedding Propagation Layers(upon GCN)

First-order propagation

和之前模型不同，这个的propagation layer encode了\(e_r\).

For entity h, the information propagating from neighbor is :

image-20230222201217039

\(π(h,r,t)\): to controls the decay factor on each propagation on edge (h,r,t), indicating how much information is propagated

from t to h conditioned to relation r.

For \(π(h,r,t)\), we use attention mechanism:

image-20230222204949423

This makes the attention score dependent on the distance between \(e^h\) and \(e^t\) in the relation r’s space.

这里，tanh用于增加非线性因素；但不缺定是否有归一化作用？？？？？归一化就可以把这个function的大小集中在角度上，但是这样\(e^h_t\)也没有归一化，到时候看看输出参数

and than use softmax to normalize(no need to use as\(\frac1{|N_t |}\)\(\frac1{|N_t ||N_h |}\))

image-20230222234256082

The final part is aggregation, threre are three choices:

  1. GCN aggregator
image-20230222235616598
  1. GraphSage aggregator
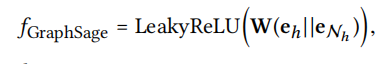
image-20230222235806956
  1. Bi-Interaction aggregator
image-20230223000647293

Multi-layer propagation

image-20230223000834658
image-20230223000850960

Model Prediction

multi-layers combination and inner product

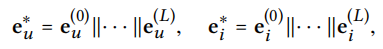
image-20230223001515690
image-20230223001526127

Optimizazion

loss

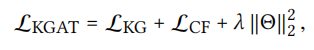
image-20230223002144083

\(L_{cf}\) is BPR Loss

image-20230223002439536

\(L_{kg}\) is loss forTranR .

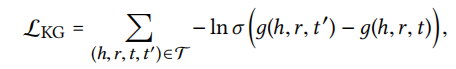
image-20230222195306105

Optimizer

Adam

updata method

we update the embeddings for all nodes;

hereafter, we sample a batch of (u,i, j) randomly, retrieve their representations after L steps of propagation, and then update model parameters by using the gradients of the prediction loss.

在同一个epoch中，先把所以数据扔进tranR训练，得到loss（此时不更新参数）

然后sample算BPR LOSS

EXPERIMENTS

RQ1: Performance Comparison

  1. regular dataset
image-20230223004843914

  1. Sparsity Levels

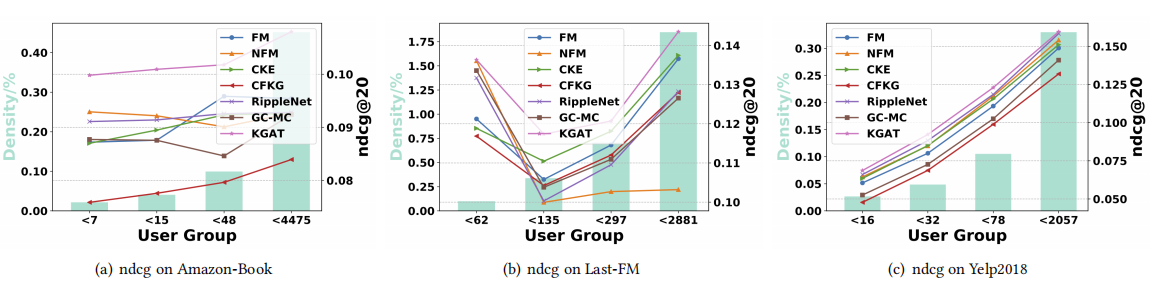
    image-20230223005253034

KGAT outperforms the other models in most cases, especially on the two sparsest user groups.

说明KGAT能够缓解稀疏性影响

RQ2：Study of KGAT

  1. study of layer influence and effect of aggregators
image-20230223010038345

  1. cut attention layer and TransR layer

    image-20230223010347815

Source code

DataProcess

Load data

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
train_data:[[u1,interacted_item1],[u1,interacted_item2],[u2,interacted_item1]]

train_user_dict:{
    user_id1:[interacted_item1,interacted_item2,...],
    user_id2:[...]
}

kg_data:[[head_e,relation,tail_e],[head_e,relation,tail_e]]

kg_dict:{
    head:[(tail,relation), (tail,relation),...]
}

relation_dict:{
    relation:[(head,tail),(head,tail),...]
}

generate the adjacency matrices and matrices after Laplacian

  1. regard interacted as relation 0, now the number of relations is \(self.n\_relations+1\)

  2. every relation \((idx)\) convert to 2 adjacency matrix (by inversing cols and rows), which representate as 2 new relations \((idx, self.n\_relations+idx)\)：

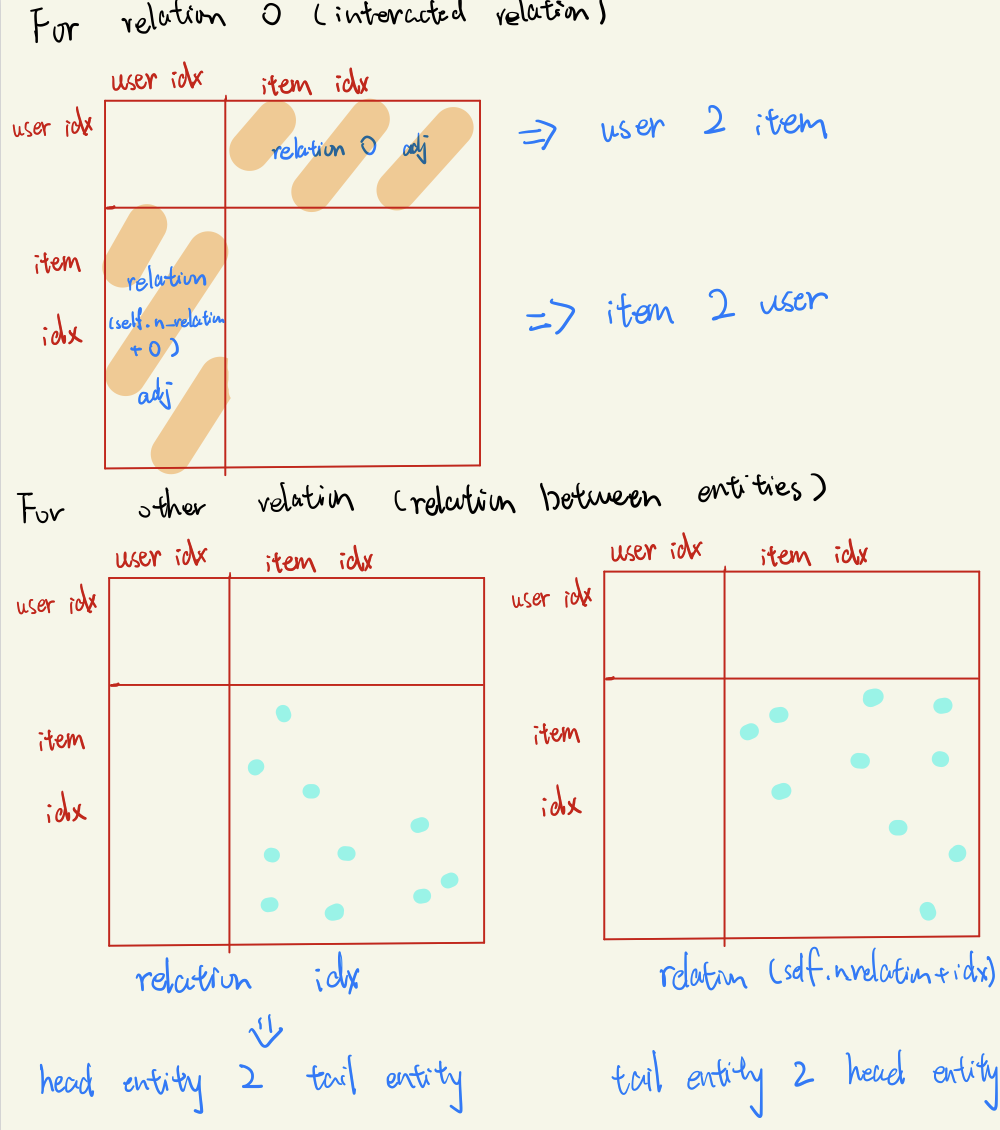
    643ED74EDA6A241DF772EA9C9435EFBD

As a result: we get adj_list, adj_r_list

1
2
3
adj_list: [adjancy matrix1, adjancy matrix2,adjancy matrix3,...]
adj_r_list: The relation adjancy matrix Correspondento to
			e.g.[0,self.n_relations+0,1,self.n_relations+1,2,self.n_relations+2,...]

Than, genarate adjancy matrix after laplacian normalization and save in self.lap_list.

Update kg dict

according to the change of relation, update kg dict

Generate batch data

build_model

Placeholder definition

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def _build_inputs(self):
    tf.compat.v1.disable_eager_execution()
    # placeholder definition
    self.users = tf.placeholder(tf.int32, shape=(None,))
    self.pos_items = tf.placeholder(tf.int32, shape=(None,))
    self.neg_items = tf.placeholder(tf.int32, shape=(None,))

    # for knowledge graph modeling (TransD)
    self.A_values = tf.placeholder(tf.float32, shape=[len(self.all_v_list)],
                                   name='A_values')

    self.h = tf.placeholder(tf.int32, shape=[None], name='h')
    self.r = tf.placeholder(tf.int32, shape=[None], name='r')
    self.pos_t = tf.placeholder(tf.int32, shape=[None], name='pos_t')
    self.neg_t = tf.placeholder(tf.int32, shape=[None], name='neg_t')

trainable weight definition

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def _build_weights(self):
    all_weights = dict()
    initializer = tf.keras.initializers.glorot_normal()

    all_weights['user_embed'] = tf.Variable(initializer([self.n_users, self.emb_dim]),
                                            name='user_embed')
    all_weights['entity_embed'] = tf.Variable(initializer([self.n_entities,
                                                           self.emb_dim]),
                                                           name='entity_embed')

    all_weights['relation_embed'] = tf.Variable(initializer([self.n_relations,
                                             self.kge_dim]),name='relation_embed')
    # E_h, E_t to E_r space
    all_weights['trans_W'] = tf.Variable(initializer([self.n_relations, 
                                                      self.emb_dim, self.kge_dim]))
    self.weight_size_list = [self.emb_dim] + self.weight_size